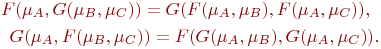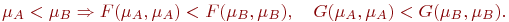The report in a subject Theoretical based information processes
«Fuzzy sets»
Done by: student “МО-424а” Ermak T. F. Checked by: Professor Yusupova N. I.
Ufa 2011 Historical information. Fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition — an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval [0, 1]. Definition. A fuzzy set is where U – universal set, Function Example. 𝑈={𝑎,𝑏,𝑐,𝑑,𝑒} 𝐴={(𝑎;0),(𝑏;0,1), (𝑐;0,5), (𝑑;0,9), (𝑒;1)} a doesn’t belong to A; b belongs to it in a small degree; c more or less belongs to A; d belongs to a large extent; e belongs to A. Example 2.
Fuzzy sets as a way of formalizing fuzzy. Maxmin: μ_(𝐴∪𝐵) (𝑥)=max〖{μ_𝐴 (𝑥),μ_𝐵 (𝑥)〗}, μ_(𝐴∩𝐵) (𝑥)=min〖{μ_𝐴 (𝑥),μ_𝐵 (𝑥)〗}; Algebraic: μ_(𝐴∪𝐵) (𝑥)=μ_𝐴 (𝑥)+μ_𝐵 (𝑥)−μ_𝐴 (𝑥) μ_𝐵 (𝑥), μ_(𝐴∩𝐵) (𝑥)=μ_𝐴 (𝑥) μ_𝐵 (𝑥); Limited: μ_(𝐴∪𝐵) (𝑥)=min{1,μ_𝐴 (𝑥) μ_𝐵 (𝑥)}, μ_(𝐴∩𝐵) (𝑥)=m𝑎𝑥〖{0,μ_𝐴 (𝑥)+μ_𝐵 (𝑥)−1〗}.
A- fuzzy set “from 5 to 8”; B – fuzzy set “near 4”
Then use maxmin operations, obtain next sets:
The carrier of a fuzzy set (supp) is a accurate set à of points in U, for which
Height of fuzzy set:
If height =1 this is normal set, else subnormal Fuzzy set is empty if The transition point of a fuzzy set A is
Types of membership function values. All fuzzy objects can be classified by type of membership function values. Apart from to the interval [0,1], membership function can approve values in interval [-1,1]. An important practical application for the formulation of quality concepts and evaluations of man in the process of solving task is the random S-fuzzy sets, where S - a finite linearly ordered set. For example, it may be a set of values of linguistic variable "QUALITY" {"bad", "medium", "good", "excellent"}. Heterogeneous fuzzy sets. When collection of fuzzy sets Then build function: Fuzzy operators. In fuzzy set theory it is possible to apply various operations of union, intersection and complement of sets depending on the context and situation. As u can see for any fuzzy sets operators 𝐹=𝑚𝑖𝑛 and 𝐺=𝑚𝑎𝑥 are the only possible intersection and union operators if the following properties: — — assotsiotivnost:
— distributivity:
— monotony:
|

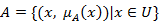 .
.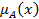 - membership function (characteristic function), characterizing the degree of membership of element x to fuzzy set A,
- membership function (characteristic function), characterizing the degree of membership of element x to fuzzy set A,  .
.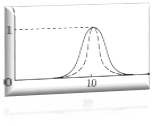 U – set of real numbers, Fuzzy set A can be defined next function of membership: μ_𝐴 (𝑥)=(1+|𝑥−10|^𝑚)^(−1); The degree of m selected based on degree of proximity to 10. For example: for numbers which so proximity to 10 it’s can be 4, not so proximity to 10 it’s can be 1or 10.
U – set of real numbers, Fuzzy set A can be defined next function of membership: μ_𝐴 (𝑥)=(1+|𝑥−10|^𝑚)^(−1); The degree of m selected based on degree of proximity to 10. For example: for numbers which so proximity to 10 it’s can be 4, not so proximity to 10 it’s can be 1or 10. Example 3
Example 3

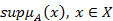
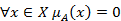

 i=1..m in X correspond m various properties of the object, each element
i=1..m in X correspond m various properties of the object, each element 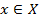 characterized vector of membership values
characterized vector of membership values  , expresses the degree of conformity to these properties.
, expresses the degree of conformity to these properties.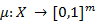 , where [0,1
, where [0,1  - full grid.
- full grid.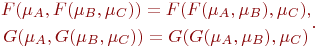 commutativity:
commutativity: