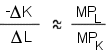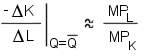An alternative derivation of the MRTS

Consider the following relationship:

This equation provides us with an approximate relationship between the change in each input and the change in output. An example might help to illustrates this. Suppose that the level of labor increases by 2 units when the marginal product of labor is 5. In this case, we'd expect to see output change by approximately 10 units. Similarly, if the MP of capital is 10, the addition of 3 extra units of output would cause output to increase by approximately 30 units. This relationship holds only approximately because changes in the level of labor or capital use result in changes in the MP of labor and capital (the law of diminishing returns is part of the explanation for this). The error will be small, though, when the changes in L and K are relatively small.

Suppose, we consider two points along an isoquant. Since output is constant (i.e., the change in Q is zero) along an isoquant, the relationship above suggests that:

Manipulating this expression a bit results in:

More precisely, since output was constrained to remain constant, this expression can be written as:

Taking the limit of this equation as the change in L becomes infinitesimally small, this becomes:

Notice that the approximate equality becomes an equality in the limit because the error in the approximation tends to zero as the changes in L and K become infinitesimally small.

A careful reader will note that the left-hand side of the equation above is equal to the definition of the MRTS. This tells us that the MRTS can also be expressed as the ratio of the MP of labor to the MP of capital. We'll make use of this result below.