Isocost curves
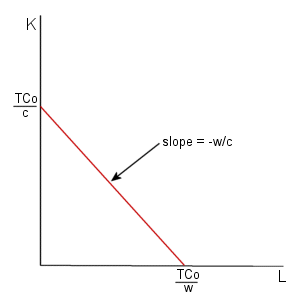
A firm's total costs in this model can be expressed as: TC = wL + cK where: TC = total cost Just as we used isoquants to represent combinations of inputs that allow the production of a given level of output, we use isocost curves to represent all of the combinations of inputs that result in a given level of total cost. The diagram below contains an isocost curve corresponding to a level of total costs equal to TCo.
Notice that the intercepts of this isocost curve equal the level of total costs divided by the price of the factor on each axis. (To demonstrate this, set the level of the other input equal to zero and solve for L or K.) The slope equals -w/c. More generally, the slope of any isocost curve relating any two factors of production will equal the price of the factor on the horizontal axis divided by the price of the factor on the horizontal axis. To see this, let's solve the total cost curve equation above for K (the variable on the vertical axis): K = (-w/c)L +(TC/c) Since this is written in standard slope-intercept form (Y = mx+b), we know that the coefficient multiplying the variable on the horizontal axis (-w/c) is the slope. The intercept on the vertical axis, as noted above, is TC/C, the constant term at the end of this expression. Any combination of inputs that lie above an isocost curve corresponds to a higher level of total costs. Combinations of inputs that lie below a total cost curve correspond to lower levels of cost. There are an infinite number of possible total cost curves. The diagram below illustrates a few such curves. Notice that all of the isocost curves are parallel to each other (since they all have a slope equal to -w/c).
Note that TC' > TCo > TC'' in this example.
|