Indifference curves and budget constraints

Let's examine how indifference curves and budget constraints may be used to illustrate the optimal combination of labor and leisure. An indifference curve is a graph of alternative combinations of goods that provide a given level of satisfaction (utility). In the simple neoclassical model of labor supply, it is assumed that the individual's utility level is a function of two goods: real income (Y), and leisure time (L). In mathematical terms, this utility function may be expressed as:

U = U(Y,L)

where U = the level of utility associated with alternative combinations of L and Y. In this case, an indifference curve provides a graph of all of the combinations of income and leisure that provides a given level of utility to an individual. The diagram below illustrates a possible indifference curve.

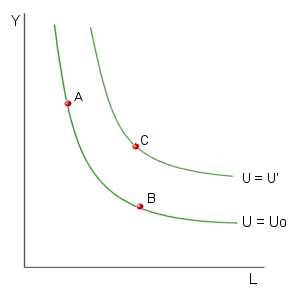
This indifference curve is downward sloping because an individual is willing to give up some income to receive additional leisure (or vice versa).

A few points have been added to the diagram below. Due to the definition of the indifference curve, this individual would be just as happy with the combination of real income and leisure represented by point A as he or she would be with the combination of Y and L represented by point B. Points that lie above and to the right of the indifference curve, such as point C, provide a higher level of utility.

Each point in this diagram provides a particular level of utility. The indifference curve that passes through point C provides a higher level of utility. This means that U' corresponds to a higher level of utility in the diagram below.