Расчет радиального ребра купола.
Наиболее напряженным будет радиальное ребро между опорным и вторым кольцами. Расчетная схема радиального ребра изображена на рисунке 7. Найдем углы наклона касательной с осью Х в уровнях опорного кольца (
Рис. 7. Расчетные схемы радиального ребра купола на нагрузки: а – горизонтальную; б – вертикальную; в – местную.
Вычислим
Для опорного радиального ребра средний угол наклона касательных:
то же для ребра между вторым и первым кольцами:
Определенная вертикальная нагрузка на опорное радиальное ребро находится:
Продольные сжимающие усилия в опорном ребре:
Суммарное продольное сжимающее усилие в опорном ребре определяется по формуле:
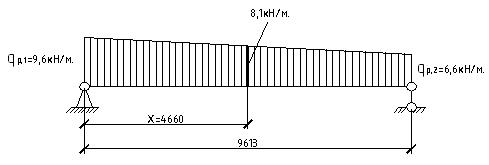
Найдем наибольшее значение изгибающего момента в опорном радиальном ребре от распределенной нагрузки (рисунок 8): Левая опорная реакция:
Рис. 8. Схема загружения опорного ребра распределенной нагрузкой.
Найдем положение сечения с наибольшим изгибающим моментом по формуле:
где
Максимальное значение изгибающего момента:
Радиальные ребра конструирую из двух прокатных швеллеров (рисунок 9), из стали марки ВСт3пс6-1 (
Рис. 9. Сечение радиального ребра. Швеллер № 30.
Считаю, что настил приваривается к радиальным и поперечным ребрам щитов, тем самым обеспечивается устойчивость ребра. Поэтому радиальное ребро буду рассчитывать только на прочность. Задаюсь швеллером №30 (
Проверяю принятое сечение радиального ребра на другую комбинацию нагрузок ( Продольные растягивающие усилия в ребре:
Распределенные нагрузки:
Поскольку интенсивность распределенной нагрузки, направленной вверх, меньше интенсивности, направленной вниз, то проверку на прочность ребра по растягивающим усилиям проводить не следует. Уточню радиус центрального кольца Длина щита верхнего яруса купола составит:
Радиальные ребра радиусов щитов испытывают меньшие нагрузки:
8.4 Расчет кольцевых элементов купола.
|

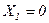 )
)  и 2-го кольца
и 2-го кольца 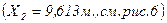 по формуле:
по формуле: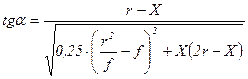 ;
; ;
; 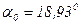 .
.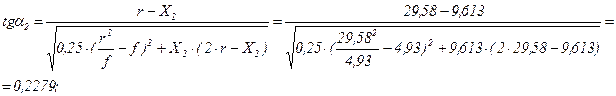
 .
. в уровне первого кольца при
в уровне первого кольца при 

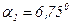 .
. ;
;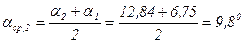 .
.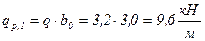 ;
;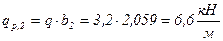 .
.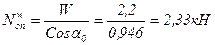 ;
;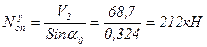 ;
;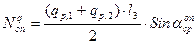 , где
, где 
 .
. .
. .
.

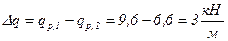
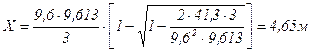 .
.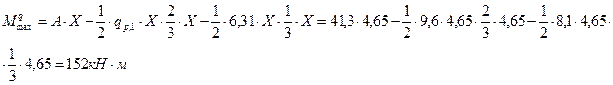
 ). Ребро работает на сжатие с изгибом, т.е. на внецентренное сжатие.
). Ребро работает на сжатие с изгибом, т.е. на внецентренное сжатие.
 ) и проверим радиальное ребро на прочность по формуле:
) и проверим радиальное ребро на прочность по формуле: 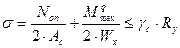 ;
;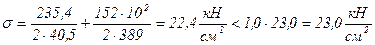 .
.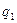 и
и 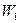 ), вызывающих растяжение.
), вызывающих растяжение.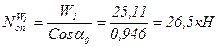 ;
; .
.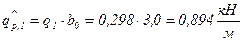 ;
; .
.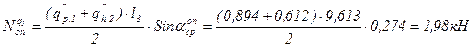 ;
;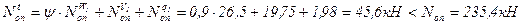 .
. из условия закрепления в нем радиальных ребер щитов из двух швеллеров № 30 (
из условия закрепления в нем радиальных ребер щитов из двух швеллеров № 30 (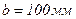 ). Учитывая, что ширина двух полок швеллера
). Учитывая, что ширина двух полок швеллера  ; толщина промежуточного ребра
; толщина промежуточного ребра  ; зазор 5мм; ширина опирания ребра составит
; зазор 5мм; ширина опирания ребра составит 
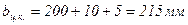 ., тогда радиус центрального кольца:
., тогда радиус центрального кольца:  .
. .
. и др. Поэтому можно оставить сечение радиальных ребер постоянным из двух швеллеров № 30.
и др. Поэтому можно оставить сечение радиальных ребер постоянным из двух швеллеров № 30.


