Когерентность и монохроматичность световых волн
Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления, т. е. вектор
где Амплитуда результирующего колебания (см. сложение колебаний в механике) в данной точке определяется:
где Когерентными называются волны, имеющие одинаковую частоту и постоянную во времени разность фаз Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Монохроматическая волна – это строго синусоидальная (косинусоидальная) волна с постоянными во времени частотой ω, амплитудой и начальной фазой. Амплитуда и фаза колебаний могут меняться от одной точки пространства к другой, а частота одна и та же во всем пространстве. Монохроматические колебания и волны длятся бесконечно долго, не имея ни начала, ни конца во времени. Поэтому строго монохроматические колебания и волны не могут быть точно реализованы в действительности – это идеализация. Строго когерентными могут быть только монохроматические волны, так как разность фаз двух монохроматических волн одинаковой частоты в каждой точке остается постоянной. В случае некогерентных волн разность фаз Тогда результирующая амплитуда равна (см. 5.1) Отсюда следует, что интенсивность света, наблюдаемая при сложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:
В случае когерентных волн
Последнее слагаемое в этой формуле называется интерференционным членом. В тех точках пространства, для которых При рассмотрении когерентности вводятся понятия временной и пространственной когерентности. Рассмотрим сначала изменение фазы с течением времени Теперь рассмотрим изменения фазы при переходе от одной точки пространства к другой. В идеальной плоской или сферической волне фаза одинакова во всех точках плоскости В реальной световой волне фаза при переходе от одной точки волновой поверхности к другой изменяется. Введем расстояние Излучение лазера обладает высокой временной и пространственной когерентностью. Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. [1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн. Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера. При интерференции энергия волн перераспределяется в пространстве. [1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. При наложении некогерентных волн средняя величина квадрата амплитуды результирующей волны равна сумме квадратов амплитуд накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий ее колебаний, обусловленных всеми некогерентными волнами в отдельности.
|

 параллелен вектору
параллелен вектору  . Тогда можно записать скалярные равенства:
. Тогда можно записать скалярные равенства: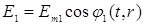
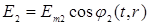 ,
, и
и  .
. , (5.1)
, (5.1) – разность фаз колебаний.
– разность фаз колебаний. . Источники таких волн также называются когерентными.
. Источники таких волн также называются когерентными. непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение
непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение 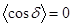 .
.
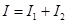
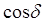 имеет постоянное во времени (но свое для каждой точки пространства) значение, так что
имеет постоянное во времени (но свое для каждой точки пространства) значение, так что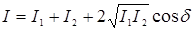 (5.2)
(5.2)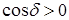 ,
,  ; в тех точках пространства, для которых
; в тех точках пространства, для которых 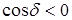 ,
,  . Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо проявляется интерференция в том случае, когда
. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо проявляется интерференция в том случае, когда  , тогда максимальная интенсивность
, тогда максимальная интенсивность  ; минимальная интенсивность
; минимальная интенсивность 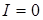 .
. в данной точке пространства. Если в данной точке пространства (
в данной точке пространства. Если в данной точке пространства ( ) в разные моменты времени разность фаз остается постоянной, то говорят о временной когерентности.
) в разные моменты времени разность фаз остается постоянной, то говорят о временной когерентности.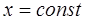 или сферы
или сферы 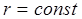 . Эти плоскости и сферы являются волновыми поверхностями.
. Эти плоскости и сферы являются волновыми поверхностями. , при смещении на которое вдоль волновой поверхности случайное изменение фазы достигает значения ~
, при смещении на которое вдоль волновой поверхности случайное изменение фазы достигает значения ~ 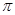 . Колебания в двух точках волновой поверхности, отстоящих друг от друга на расстояние, меньшее
. Колебания в двух точках волновой поверхности, отстоящих друг от друга на расстояние, меньшее 


