Силы дисперсионного взаимодействия
Энергия дисперсионного взаимодействия двух сферических частиц описывается уравнением Лондона:
где k - коэффициент пропорциональности, зависящий от потенциала ионизации частиц; a1, a2 - поляризуемость частиц; r - расстояние между частицами. Поскольку каждая частица обладает определенной поляризуемостью, дисперсионные силы проявляются при взаимодействии любых частиц. В растворах органических соединений дисперсионные силы вносят основный вклад в энергию межмолекулярного взаимодействия, а для неполярных молекул только они обуславливают меж- молекулярные взаимодействия. Поляризуемость частиц a в первом приближении можно выразить через молекулярную рефракцию RM соотношением:
в котором n – показатель преломления исследуемого соединения; М – его молярная масса; d - плотность; N – число Авогадро. Минимально возможные расстояния между частицами определяются как сумма ван-дер-ваальсовых радиусов этих частиц. Однако достаточно точное вычисление энергии дисперсионных сил даже для простейших систем осложнено тем, что определение реальных расстояний между частицами существенно затруднено. Выходом из создавшегося положения может быть использование правила аддитивности для расчета дисперсионного взаимодействия молекул как суммы инкрементов отдельных атомов, входящих в состав этих молекул. Каждый атом или атомная группа обладают легко находимой по справочнику атомной рефракцией. Однако атомы и атомные группы экранируются внутри молекулы ближайшими частицами. Вследствие такого экранирования лишь часть поверхности атомной группы взаимодействует с окружающей средой. Эту часть можно определить для любой группы атомов или отдельных атомов, что дает возможность рассчитать для каждой группы коэффициент внутримолекулярного экранирования в зависимости от размеров ближайших частиц. Из уравнения (84) видно, что энергия дисперсионного взаимодействия уменьшается пропорционально шестой степени расстояния между частицами и поэтому без больших ошибок можно ограничиться рассмотрением взаимодействия между двумя наиболее близко расположенными атомными группами сорбата и неподвижной фазы. В этом случае соблюдаются основные условия использования уравнения.
|

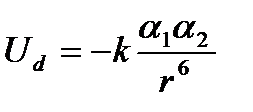 , (84)
, (84) , (85)
, (85)


