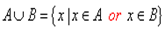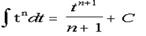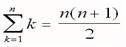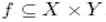MATHEMATICAL LANGUAGE

There are many symbols in mathematics and most are used as a precise form of shorthand. We need to be confident when using these symbols, and to gain that confidence we need to understand their meaning. To understand their meaning there are two things to help us: context - this is the context in which we are working, or the particular topics being studied, and convention - where mathematicians and scientists have decided that particular symbols will have particular meaning.

Words associated with the symbol “+” are ‘plus’, ‘add’, ‘increase’ and ‘positive’. Words associated with the symbol “−” are ‘minus’, ‘ subtract ’, ‘take away’, ‘negative’ and ‘decrease’. Generally we use these two common signs to add or subtract something. The symbols “++” and “- -“ are used as an increment and a decrement in imperative programming languages.

Multiplication is the mathematical operation of scaling one number by another. Words associated with the symbol "×" are ‘ multiply ’, ‘lots of’, and ‘times’. Because the result of scaling by whole numbers can be thought of as consisting of some number of copies of the original, whole-number products greater than 1 can be computed by repeated addition; for example, 3 multiplied by 4 (often said as "3 times 4") can be calculated by adding 4 copies of 3 together:

3×4 = 3+3+3+3 = 12

Here 3 and 4 are the " factors " and 12 is the " product ".

In mathematics, especially in elementary arithmetic, division (÷) is an arithmetic operation. In the expression a ÷ b = c, a is called the dividend or numerator, b the divisor or denominator and the result c is called the quotient. Dividing two integers may result in a remainder. To complete the division of the remainder, the number system is extended to include fractions or rational numbers as they are more generally called.

Another symbol used frequently is the equals sign “=”. The “=” sign does not mean anything on its own - we need a context. For example, in the sum 1+2 = 3, what we are saying is that whatever we have on the left-hand side is exactly equal to whatever we have on the right-hand side.

Variations of the equals sign are:

≠ which means ‘is not equal to’;

≈ which means ‘is approximately equal to’;

≥ which means ‘is greater than or equal to’;

≤ which means ‘is less than or equal to’.

In computer science, the mentioned above signs belong to relational operators that test or define some kind of relation between two entities. In programming languages that include a distinct boolean data type in their type system, like Java, these operators return true or false, depending on whether the conditional relationship between the two operands holds or not. In other languages such as C, relational operators return the integers 0 or 1.

In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and its applications. In computer programming, a variable is a storage location and an associated symbolic name (an identifier) which contains some known or unknown quantity or information, a value. The variable name is the usual way to reference the stored value; this separation of name and content allows the name to be used independently of the exact information it represents. The identifier in computer source code can be bound to a value during run time, and the value of the variable may thus change during the course of program execution. Variables in programming may not directly correspond to the concept of variables in mathematics. The value of a computing variable is not necessarily part of an equation or formulas in mathematics. In computing, a variable may be employed in a repetitive process: assigned a value in one place, then used elsewhere, then reassigned a new value and used again in the same way (iteration). Variables in computer programming are frequently given long names to make them relatively descriptive of their use, whereas variables in mathematics often have one- or two-character names for brevity in transcription and manipulation.

The positioning of numbers and symbols in relation to each other also gives meaning. For example, you will come across use of superscripts. These are small numbers or symbols written at the top right of another, as in 4². In this context 4² is a shorthand for ‘four squared ’ or 4 x 4. Similarly 4³ is shorthand for ‘four cubed ’ or 4 x 4 x 4. On the other hand 32° can mean different things in different contexts. It might mean an angle of 32 degree s. It could mean 32 to the power zero, which is actually 1.

2. Find English equivalents in the text:

Умовне позначення, норма (домовленість), певні символи, віднімати, унарний оператор, компонент операції, який піддається зміні, показники, суміжний, першочерговий, обчислення, множити, повторюване додавання, множники, добуток, ділене, дільник, частка, остача, дроби, знак рівності, наближено, оператори рівності, умовний, змінна, місце розташування, значення, посилатися на, ідентифікатор, призначати нову величину (значення), повторення, стислість, надрядковий індекс, підносити до квадрата, підносити до куба, кут, градус, степінь.

 

3. What is meant by the following definitions? Choose the words from the databank:

Databank: a convention, a superscript, brevity, a constant, an angle, a sign, unary operation, a factor, a variable, power.

1) the most widely accepted or established view; 2) a conventional figure or device that stands for a word, phrase, or operation; 3) a mathematical operation, such as the square root function and complex conjugation, that requires only one operand; 4) one of two or more integers or polynomials whose product is a given integer or polynomial; 5) a quantity assumed to have a fixed value in a specified mathematical context; 6) a quantity capable of assuming any of a set of values; 7) conciseness of expression; 8) a character set, printed, or written above and immediately to one side of another; 9) the figure formed by two lines diverging from a common point; 10) the value of a number or quantity raised to some exponent.

4. Read the formulae. Consult Appendix 6:

a)

 

b)

c)

 

d)

 

e)

 

f)

 

g)

5. Match the terms with their definitions:

1. addition	a) The operation of determining how many times one quantity is contained in another; the inverse of multiplication.
2. subtraction	b) A statement, usually an equation, that one thing equals another.
3. multiplication	c) The branch of mathematics that deals with limits and the differentiation and integration of functions of one or more variables.
4. di­vision	d) An expression that indicates the quotient of two quantities.
5. equality	e) The act or process of adding, especially the process of computing with sets of numbers so as to find their sum.
6. fraction	f) The act or process of multiplying or the condition of being multiplied.
7. whole num­ber	g) A mathematical operation in which the difference between two numbers or quantities is calculated.
8. cal­culus	h) An equation containing differentials or derivatives of a function of one independent variable.
9. differential equations	i) A self-evident or universally recognized truth.
10. theorem	j) A member of the set of positive integers and zero.
11. axioms	k) A proposition that has been or is to be proved on the basis of explicit assumptions.

6. Answer the questions:

1. What does the understanding of mathematical symbols depend on?

2. How can the symbols “+” and “−” be used in computing?

3. What is multiplication? What terms are common for this operation?

4. What is division? What terms are common for this operation?

5. What are the variations of the equals sign?

6. What is the difference in understanding of the concept “variable” in mathematics and computer science?

7. What is a superscript? What can 32° mean?

7. Read and translate the text: