Раздел 1 ОСНОВЫ АЛГОРИТМИЗАЦИИТема 1.1 Этапы решения задачи на ЭВМ. Понятие и свойства алгоритма. Алгоритмы и величины (2) Этапы решения задачи на ЭВМ. Работа по решению любой задачи с использованием компьютера делится на следующие этапы: 1. Постановка задачи. 2. Формализация задачи (математическая формулировка). 3. Математическая формулировка 4. Построение алгоритма. 5. Составление программы на языке программирования. 6. Отладка и тестирование программы. 7. Проведение расчетов и анализ полученных результатов. Часто эту последовательность называют технологической цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5. На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения, и тип (вид) необходимого результата (число, символ, строка, ряд чисел, график, рисунок, файл и т.д.) Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели. Третий этап определяет численный математический метод, позволяющий свести решение задачи к последовательному выполнению основных четырех арифметических действий. В некоторых случаях одна и та же задача может решаться несколькими численными методами. Например, квадратное уравнение можно решить: через дискриминант, с помощью теоремы Виета, графическим способом. Таким образом, необходимо выбрать метод, наилучшим образом обеспечивающий выполнение требований поставленной задачи. Кроме того, на данном этапе необходимо найти все частные случаи, то есть случаи, когда задача не имеет решений, или решения выполняется по другой формуле (другим методом) и определить порядок рассмотрения этих случаев. Четвертый этап — построение алгоритма. Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования. Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования. Последний (шестой) этап — это использование уже разработанной программы в практических целях. Таким образом, программист должен обладать следующими знаниями и навыками: • уметь строить алгоритмы; • знать языки программирования; • уметь работать в соответствующей системе программирования. Основой программистской грамотности является развитое алгоритмическое мышление.
Понятие алгоритма. Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithm! — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам. В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем. В школьном курсе информатики с понятием алгоритма, с методами построения алгоритмов ученики знакомятся на примерах учебных исполнителей: Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке. Алгоритм - четкое описание последовательности действий, которые необходимо выполнить для решения задачи. Разработать алгоритм означает разбить задачу на последовательно выполняемые шаги (этапы). При этом должны быть четко указаны не только содержания этапов, но и порядок их выполнения. Отдельный этап (шаг) алгоритма представляет собой либо другую более простую задачу, алгоритм которой разработан ранее, либо достаточно прост и без пояснения. Свойства алгоритмов: - Дискретность - это свойство состоит в том, что алгоритм должен представлять процесс решения задачи, как последовательное выполнение простых шагов. При этом для выполнения каждого шага требуется некоторый конечный отрезок времени. То есть преобразование исходных данных осуществляется по времени дискретно. - Детерминированность (определенность) - означает однозначное толкование элементов алгоритма. Его многократное исполнение при одних и тех же исходных данных должно приводить к одному и тому же результату. - Результативность алгоритма заключается в возможности получения определенного результата для допустимых данных за конечное число шагов. - Универсальность или массовость алгоритма означает, что его возможно применять при любых допустимых исходных данных. Если для данной задачи не возможно составить алгоритм, обладающий данными свойствами, то задача является алгоритмически неразрешимой и не может быть решена на ЭВМ.
В разделе информатики под названием «Программирование» изучаются методы программного управления работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер. Компьютер работает с величинами — различными информационными объектами: числами, символами, кодами и т. п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами. Данные и величины. Совокупность величин, с которыми работает компьютер, принято называть данными. По отношению к программе данные делятся на исходные, результаты (окончательные данные) и промежуточные (рис. 1), которые получаются в процессе вычислений.
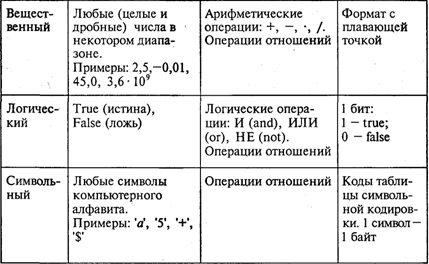
Например, при решении квадратного уравнения ax2 + bx + с = 0 исходными данными являются коэффициенты а, b, с, результатами — корни уравнения х1, х2, промежуточным данным — дискриминант уравнения D = b2 — 4aс. Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина занимает свое определенное место в памяти ЭВМ (иногда говорят — ячейку памяти). Хотя термин «ячейка» с точки зрения архитектуры современных ЭВМ несколько устарел, однако в учебных целях его удобно использовать. У всякой величины имеются три основных свойства: имя, значение и тип. На уровне команд процессора величина идентифицируется при помощи адреса ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные Константа — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, k, true и т.д. Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, codl5. Любая константа, как и переменная, занимает ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке. Теперь о типах величин — типах данных. С понятием типа данных вы уже, возможно, встречались, изучая в курсе информатики базы данных и электронные таблицы. Это понятие является фундаментальным для программирования. В каждом языке программирования существует своя концепция типов данных, своя система типов. Тем не менее в любой язык входит минимально необходимый набор основных типов данных, к которому относятся: целый, вещественный, логический и символьный типы. С типом величины связаны три ее характеристики: - множество допустимых значений, - множество допустимых операций, - форма внутреннего представления. В табл. 1.1 представлены эти характеристики основных типов данных. Таблица 1.1
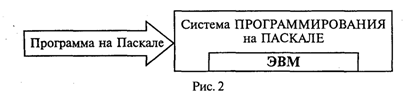
Типы констант определяются по контексту (т. е. по форме записи в тексте), а типы переменных устанавливаются в описаниях переменных. Есть еще один вариант классификации данных — классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина — одно значение, для структурированных: одна величина — множество значений. К структурированным величинам относятся массивы, строки, множества и т.д. ЭВМ — исполнитель алгоритмов. Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя в рамках его системы команд. О каком же исполнителе идет речь при обсуждении вопроса о программировании для ЭВМ? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс: ЭВМ + Система программирования (СП). Программист составляет программу на том языке, на который ориентирована СП. Иногда в литературе такой комплекс называют виртуальной ЭВМ. Например, компьютер с работающей системой программирования на Бэйсике называют Бэйсик-машиной; компьютер с работающей системой программирования на Паскале называют Паскаль-машиной и т.п. Схематически это изображено на рис. 2.
Входным языком такого исполнителя является язык программирования Паскаль.
Тема 1.2 Запись алгоритма в виде блок–схем (2)
Независимо от того, на каком языке программирования будет написана программа, алгоритм решения любой задачи на ЭВМ может быть составлен из команд: • присваивания; • ввода; • вывода; • обращения к вспомогательному алгоритму (подпрограмме); • цикла; • ветвления (условия). Запись алгоритма производится в наглядной и компактной форме, удобной для практического использования. Наибольшее распространение получила графическая запись структуры алгоритмов в виде блок-схем, то есть последовательности специальных символов (блоков), каждому из которых соответствует определенный этап решения задачи. Блоки соединяются линиями потока информации. Начало или конец программы обозначаются блоком:
Линии, соединяющие между собой блоки в блок–схеме, называются линиями потока информации и обозначаются (стрелка обязательна, так как она показывает направление перемещения информации): Любое вычисление или присваивание обозначаются блоком:
Например:
или
Из данного вида блока может выходить только одна линия потока информации, соответствующая следующему этапу алгоритма, хотя входить в данных блок их может несколько.
Ввод исходных данных (обычно с клавиатуры) или печать результата вычислений (обычно на экран) обозначаются блоком: Например:
или или
Из данного вида блока также может выходить только одна линия потока информации, соответствующая следующему этапу алгоритма, хотя входить в данных блок их может несколько. Проверка условия или ветвление обозначаются блоком:
Например:
или
Из блока обозначающего условие (ветвление) должно выходить две линии, соответствующие последовательности действий, которые необходимо выполнить в истинности (выполнения) и ложности (невыполнения) условия соответственно. Например:
или
Обычно циклические алгоритмы организуются с помощью условий, для цикла со счетчиком существует особый блок:
Подробно изучим его в теме «Циклические алгоритмы». Довольно часто алгоритмы получаются большими и не умещаются на одном листе. Чтобы корректно продолжить алгоритм на новом листе используют перенос на следующую страницу:
Например, к конце страницы ставиться:
а в начале следующей страницы:
Обращение к вспомогательному алгоритму (вызов подпрограммы) обозначается следующим образом.
Например, вызов подпрограммы Степень:
Для описания алгоритмов в дальнейшем мы будем использовать блок-схемы и учебный алгоритмический язык, применяемый в школьном курсе информатики. Тема 1.3 Линейные вычислительные алгоритмы (2) Основным элементарным действием в вычислительных алгоритмах является присваивание значения переменной величине. Если значение константы определено видом ее записи, то переменная величина получает конкретное значение только в результате присваивания. Присваивание может осуществляться двумя способами: с помощью команды присваивания и с помощью команды ввода. Рассмотрим пример. Вычислить значение функции F=357-a*b Построим алгоритм вычисления данной функции для ЭВМ. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются числовые переменные а, b. Результатом — числовая величина F. Блок-схема и текст алгоритма на учебном алгоритмическом языке приведены ниже (в дальнейшем для краткости будем обозначать учебный алгоритмический язык буквами АЯ).
алг Вычисление функции нач вещ a,b,F ввод a, b m:=a*b F:=357-m вывод F кон
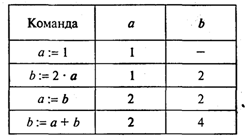
Формат команды присваивания следующий: переменная:=выражение Знак «:=» нужно читать как «присвоить». Команда присваивания обозначает следующие действия, выполняемые компьютером: 1. Вычисляется выражение. 2. Полученное значение присваивается переменной. В приведенном выше алгоритме присутствуют две команды присваивания. В блок-схемах команда присваивания записывается в прямоугольнике. Такой блок называется вычислительным блоком. В описаниях алгоритмов необязательно соблюдать строгие правила в записи выражений. Их можно писать в обычной математической форме. Это еще не язык программирования со строгим синтаксисом. В приведенном алгоритме присутствует команда ввода: ввод a, b В блок-схеме команда ввода записывается в параллелограмме — блоке ввода-вывода. При выполнении данной команды процессор прерывает работу и ожидает действий пользователя. Пользователь должен набрать на устройстве ввода (клавиатуре) значения вводимых переменных и нажать на клавишу ввода Enter. Значения следует вводить в том же порядке, в каком соответствующие переменные расположены в списке ввода Обычно с помощью команды ввода присваиваются значения исходных данных, а команда присваивания используется для получения промежуточных и конечных величин. Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для этих целей предназначена команда вывода: вывод F С помощью этой команды результаты выводятся на экран или на устройство печати на бумагу. Поскольку присваивание является важнейшей операцией в вычислительных алгоритмах, обсудим ее более подробно. Рассмотрим последовательное выполнение четырех команд присваивания, в которых участвуют две переменные величины а и b. В приведенной ниже таблице напротив каждой команды присваивания указываются значения переменных, которые устанавливаются после ее выполнения.
Этот пример иллюстрирует три основных свойства команды присваивания: • пока переменной не присвоено значение, она остается неопределенной; • значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующей команды присваивания этой переменной; • новое значение, присваиваемое переменной, заменяет ее предыдущее значение. Рассмотрим один очень полезный алгоритм, который приходится часто использовать при программировании. Даны две величины: X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было Х = 1, Y = 2, то после обмена должно стать: Х = 2, Y = 1. Хорошей моделью для решения этой задачи является следующая ситуация: имеются два стакана — один с молоком, другой с водой. Требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: 1) перелить из первого стакана в третий; 2) перелить из второго в первый; 3) перелить из третьего во второй. Цель достигнута! По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача обмена решается последовательным выполнением трех команд присваивания:
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х: = Y) переменная, стоящая справа (Y), сохраняет свое значение. Алгоритм для вычисления значения указанной выше функции имеет линейную структуру. В нем все команды выполняются в строго однозначной последовательности, каждая по одному разу. Линейный алгоритм составляется из команд присваивания, ввода, вывода и обращения к вспомогательным алгоритмам (подпрограммам). При описании алгоритмов в блок-схемах типы, как правило, не указываются (но подразумеваются). В алгоритмах на АЯ для всех переменных типы указываются явно. Описание типов переменных производится сразу после заголовка алгоритма. В них используются следующие обозначения типов: цел — целый тип, вещ — вещественный тип, лит — символьный (литерный) тип, лог — логический тип. В алгоритме для вычисления значения функции для всех переменных указан вещественный тип, так как и аргументы и результат функции могут быть любыми числами (целыми, нецелыми, положительными, отрицательными и т.д.). Таблица выполнения для данного алгоритма (пусть с клавиатуры ввели a=4, b=-1):
Задание: для следующих задач построить блок-схему, написать текст алгоритма и построить таблицу выполнения (исходные данные, вводимые с клавиатуры, задайте самостоятельно): 1. Вычислите путь, пройденный телом при равноускоренном движении: 2. Вычислите значение функции f=dx2+cx 3. Вычислите значение функции f=a(x2+c)x
Тема 1.4 Разветвляющиеся (условные) алгоритмы (4) На практике линейный тип алгоритма встречается редко при решении простейших задач, не имеющих частных случаев. Напомним, что частные случаи – это случаи, когда задача не имеет решений, или решения выполняется по другой формуле (другим методом). Например, при вычислении функции Разветвляющийся (условный) алгоритм содержит блоки проверки какого-либо условия, и в зависимости от результатов проверки выполняется та или иная последовательность операций, называемая ветвью. С помощью таких алгоритмов решаются задачи, имеющие в методе решения хотя бы один частный случай.
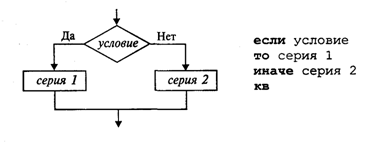
Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется серия 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется серия 2 (отрицательная ветвь). В АЯ условие записывается после служебного слова если, положительная ветвь — после слова то, отрицательная — после слова иначе. Буквы кв обозначают конец ветвления.
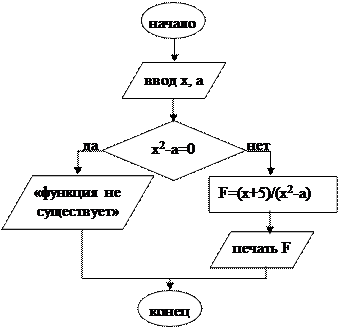
алг Вычисление функции 2 нач вещ x, a, F ввод x, a если x2-a=0 то вывод «функция не существует» иначе F:=(x+5)/(x2-a) вывод F кв кон
Рассмотрим результаты работы алгоритма при следующих данных: x=1, a=1.Построим таблицу выполнения:
Обратите внимание, что при указанных исходных данных, функция так и не была вычислена (переменная F не получила значения), так так знаменатель функции равен 0. Рассмотрим результаты работы алгоритма при других данных: x=2, a=1.Построим таблицу выполнения:
Поскольку знаменатель функции не равен 0 (условие не выполнилось), переменная F получила значение. При вычислении по формулам чаще всего возникают следующие частные случаи, обусловленные правилам арифметических действий (нельзя делить на 0, вычислять корень из отрицательных чисел и т.д.): · знаменатель =0 (рассмотрено выше); · подкоренное выражение меньше 0; · аргумент логарифма меньше или равен 0; · при вычислении тангенса необходимо помнить, что данная функция не существует, если косинус данного алгоритма равен 0; · при вычислении котангенса необходимо помнить, что данная функция не существует, если синус данного алгоритма равен 0; · геометрические измерения (стороны фигур, радиусы и т.д.), физические (емкости, пути, сила тока и т.д.) величины как правило не могут быть меньше или равны 0 и могут подчиняться специальным правилам (например, сумма углов треугольника должна быть равна 180°);
Задача может иметь несколько частных случаев. Рассмотрим пример: вычислите значение функции Частные случаи следующие: · · x – c < 0 – подкоренное выражение меньше 0 Порядок рассмотрения частных случаев очень важен. Если мы будем рассматривать частные случаи, в том порядке, как они указаны выше, то сначала необходимо вычислить знаменатель и убедиться, что он не равен нулю, но для этого придется вычислить квадратный корень из x – c, а нам не известно чему равно подкоренное выражение, поэтому при x=1, c=5 возникнет ошибка при проверке условия. Порядок рассмотрения частных случаев определяется следующим образом: 1. определите порядок действий в выражении, 2. арифметические действия или функции проверяются в том порядке, в котором они вычисляются Для нашей задачи порядок проверки частных случаев следующий: 1. x – c < 0 2. Блок-схема и текст алгоритма на учебном алгоритмическом языке приведены ниже: алг Вычисление функции 3 нач вещ x, d, c, F ввод x, d, c если x-c<0 то вывод «функция не существует» иначе если вывод «функция не существует иначе
вывод F кв кв кон
Обратите внимание, что оба частных случая приводят к одинаковому результату – печать строки. В таких случаях можно объединить условия в одно сложное условие с помощью логических операторов. Наиболее часто используются логические операторы ИЛИ, И, НЕ.
|
Например:
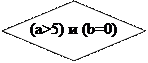
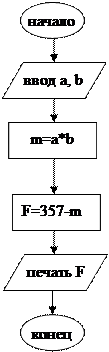
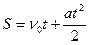
, если знаменатель равен 0, то функция не существует. Следовательно, при x2-a=0 функция не существует – это частный случай. Задачи, имеющие частные случай, решаются с помощью разветвляющихся (условных) алгоритмов.
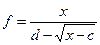, функция не существует, если x-c<0
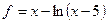, функция не существует, если x-5<=0
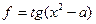, данную формулу можно записать следующим образом 
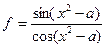, в знаменателе оказывается cos(x2-a), следовательно, при cos(x2-a)=0 функция не существует
, данную формулу можно записать следующим образом 
, в знаменателе оказывается sin(x2-a), следовательно, при sin(x2-a)=0 функция не существует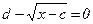
- знаменатель равен 0
