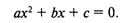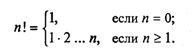Обратите внимание, что внутри сложного условия (состоящего из нескольких частей) условия записываются в порядке проверки частных случаев.
Если необходимо, чтобы выполнялись оба найденных условия, они соединяются с помощью оператора И. Когда необходимо, что выполнялось хотя бы одно из этих условий, условия соединяются с помощью союза ИЛИ. Оператор НЕ (отрицание) используется для того, чтобы обратить значение условия на противоположное. Рассмотрим логические операторы подробнее. Логическое ИЛИ используется в тех случаях, когда условие должно быть верно, если хотя бы одна из частей условия верна. Например, треугольник не существует, если хотя бы одна из сторон отрицательна или равна 0. Условие запишется следующим образом: (A <= 0) ИЛИ (В <= 0) ИЛИ (С <= 0) Логическое И используется в тех случаях, когда условие должно быть верно, если все части условия верны. Например, треугольник существует, если все его стороны положительны, то есть и A > 0 и B > 0 и C > 0. Условие запишется следующим образом: (A > 0) И (B > 0) И (C > 0) Отдельно стоит логический оператор НЕ (отрицание). Его часто используют, чтобы "обратить условие", то есть сменить значение условия на противоположное. Например, если есть условие A > 0, то НЕ (A > 0) означает "A не больше нуля", то есть меньше или равно нуля. Конечно простые условия, состоящие из одной части, легко обратить просто изменив знак отношения на противоположный (Например, вместо A > 0 записать A <= 0). Но если требуется обратить сложное условие, состоящее из нескольких частей, в условие необходимо вносить слишком много изменений, что повышает вероятность ошибки. Например, что бы обратить условие (A = 5) И (B <> 0) ИЛИ (C > 10) необходимо сделать следующие изменения ((A <> 5) ИЛИ (B = 0)) И (С < 10) Естественно, гораздо проще написать НЕ ((A = 5) И (B <> 0) ИЛИ (C > 10)) Поговорим о приоритете логических операторов: 1) действия в скобках 2) оператор НЕ 3) оператор И 4) оператор ИЛИ Так как действия в скобках имеют наивысший приоритет, следовательно, расстановка скобок может изменить смысл всего условия. Например: ((A > 0) И (B > 0)) ИЛИ (C < 0) и (A < 0) И ((B > 0) ИЛИ (C < 0))
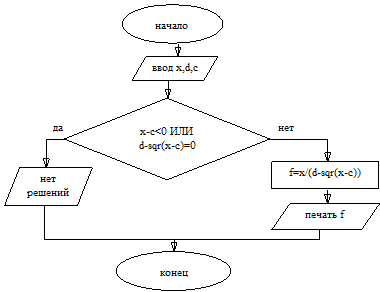
Для нашей задачи объединим частные случаи в одно сложное условие: очевидно, что функция не существует если выполняется хотя бы один частные случай, то есть используем оператор ИЛИ:
алг Вычисление функции 3 нач вещ x, d, c, F ввод x, d, c если (x-c<0) ИЛИ ( вывод «функция не существует» иначе
вывод F кв кон
Разберем следующие примеры:
Пример 1. Вычислите площадь треугольника по формуле: При То есть при ( А при( Задание: самостоятельно создайте блок-схему алгоритма и запись алгоритма на АЯ
Пример 2. Вычислите значение функции: При вычислении нашей функции частные ситуации (в данному случае - функция не существует) возникнут в следующих случаях: 1) 2) 3) 4) 5) При определении порядка рассмотрения частных случаев при вычислении функций руководствуемся порядком выполнения действий при вычислении выражения. То есть в каком порядке вычисляется выражение, в том же порядке рассматриваются частные случаи: 1) 2) 3) 4) 5) Задание: самостоятельно создайте блок-схему алгоритма и запись алгоритма на АЯ
Задания: Для следующих задач найти частные случаи, определить их порядок, составить блок-схему алгоритма и запись алгоритма на АЯ: 1. Вычислите значение функции: 2. Вычислите объемов цилиндра основания R и высотой Н: 3. Вычислите значение функции: 4. Вычислите значение функции: 5. Вычислите значение функции: 6. Вычислите значение функции: 7. Вычислите медиану, опущенную на сторону а, по известным сторонам треугольника a, b, c: (обратите внимание на условие существования треугольника) 8. Вычислите значение функции: 9. Вычислите значение функции: 10. Вычислите объем шарового слоя 11. Вычислите значение функции:
Тема 1.5 Вложенные условия (2)
Рассмотрим применение вложенных операторов на следующем примере: вычислите значение функции Обратите внимание, что при х<=2, функций не существует при x<0, так как квадратный корень из отрицательных чисел вычислять нельзя. Следовательно, необходимо применить вложенный условный оператор, чтобы отследить случаи, когда функций не существует. Блок-схема алгоритма и запись алгоритма на АЯ приведены ниже:
алг Вычисление функции 4 нач вещ x ввод x если x>2 то f=x2 вывод F иначе если x<0 то вывод «функция не существует» иначе
вывод F кв кв кон
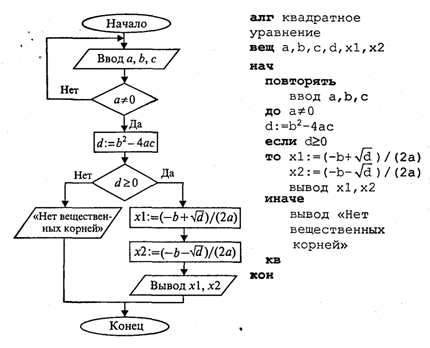
Рассмотрим алгоритм решения квадратного уравнения
Задача хорошо знакома из математики. Допустим, решаем через дискриминант. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня x1 и х2, которые вычисляются по формуле:
Все используемые в этой программе величины вещественного типа.
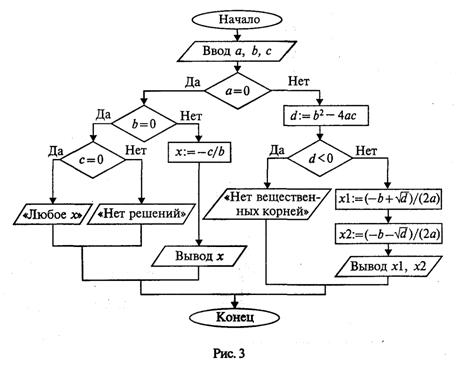
Слабость такого алгоритма видна невооруженным глазом. Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам, — универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат). Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи. Решение уравнения зависит от значений коэффициентов a, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней): если a = 0, b = 0, с = 0, то любое х — решение уравнения; если а = 0,b = 0, с ≠ 0,то уравнение действительных решений не имеет; если а = 0, b ≠ 0, то это линейное уравнение, которое имеет одно решение х = -с/b; если a ≠ 0 и d = b2- 4ас ≥ 0, то уравнение имеет два вещественных корня (формулы приведены выше); если а ≠ 0 и d < 0, то уравнение не имеет вещественных корней. Блок-схема алгоритма приведена на рис. 3.
Этот же алгоритм на алгоритмическом языке:
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «Корни квадратного уравнения».
Практическая работа 1 Поиск частных случаев. Создание разветвляющихся алгоритмов
Тема 1.6 Циклические алгоритмы (4)
Циклический алгоритм содержит некоторую последовательность операций, выполняемую многократно в зависимости от выполнения какого-либо условия. Существуют 3 типа структур цикла.
Цикл с предусловием Цикл с постусловием Цикл с повторением
Цикл с предусловием – в начале цикла проверяется условие; если оно верно, выполняются операторы, находящиеся внутри цикла, цикл повторяется, пока условие верно. Отличительной особенностью данного вида цикла является то, что он может не выполниться ни разу, если при входе в цикл условие изначально не верно. Цикл с постусловие – в начале выполняются операторы, находящиеся внутри цикла, а затем проверяется условие; операторы повторяются, если условие верно. Отличительной особенностью данного вида цикла является то, что он обязательно выполниться хотя бы один раз, так как условие проверяется в конце. Цикл со счетчиком – выполняется заданное количество раз. Задается начальное и конечное значение счетчика цикла, а также шаг его изменения. Выполнение цикла прекращается, когда счетчик достигает конечного значения.
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала:
Факториал представляет собой произведения натуральных чисел n!=1*2*3*…*n. Следовательно, необходимо в цикле перемножать числа, начиная с 1, пока текущее число не меньше или равно n. Попробуем решить данную задачу с помощью цикла с предусловием, который работает следующим образом: в начале цикла проверяется условие; если оно верно, выполняются операторы, находящиеся внутри цикла, цикл повторяется, пока условие верно. Отличительной особенностью данного вида цикла является то, что он может не выполниться ни разу, если в момент входа в цикл условие неверно.
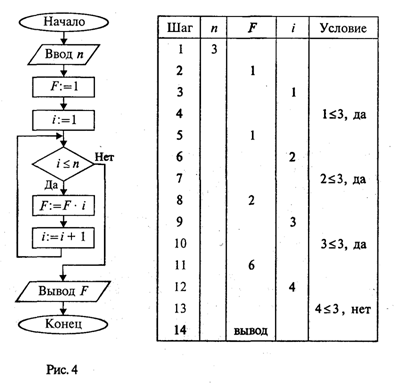
На следующем рисунке приведена блок-схема алгоритма. В нем используются три переменные целого типа: n — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица (таблица исполнения). В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n = 3.
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда цикл-пока, или цикл с предусловием. Общий вид команды цикл-пока в блок-схемах и в АЯ следующий:
пока условие, повторять нц серия кц Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова нц и кц обозначают начало цикла и конец цикла соответственно. Цикл с предусловием — это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля — еще один признак хорошего качества программы.
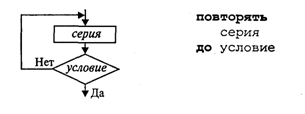
В общем виде структурная команда цикл с постусловием или цикл—до представляется так:
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу. Составим алгоритм решения следующей задачи: даны два натуральных числа М и N. Требуется вычислить их наибольший общий делитель — НОД(М, N). Эта задача решается с помощью метода, известного под названием алгоритма Евклида Его идея основана на том свойстве, что если M > N, то НОД(М, N) = НОД(М — N,N). Попробуйте самостоятельно доказать это свойство. Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, M) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции: 1. Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма. 2. Определить большее из чисел. 3. Заменить большее число разностью большего и меньшего значений. 4. Вернуться к выполнению пункта 1. Блок-схема и алгоритм на АЯ будут следующими:
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая М = 18, N = 12. В результате получится НОД = 6, что, очевидно, верно. Тема 1.7. Вспомогательные алгоритмы и процедуры (2) В теории алгоритмов известно понятие вспомогательного алгоритма. Вспомогательным называется алгоритм решения некоторой подзадачи из основной решаемой задачи. В таком случае алгоритм решения исходной задачи называется основным алгоритмом. В качестве примера рассмотрим следующую задачу: требуется составить алгоритм вычисления степенной функции с целым показателем у = хk, где k — целое число, х ≠ 0. В алгебре такая функция определена следующим образом:
Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень. Учитывая, что 1/х-n = (1/х) -n, запишем основной алгоритм решения этой задачи.
Здесь дважды присутствует команда обращения к вспомогательному алгоритму с именем СТЕПЕНЬ. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами. В учебном алгоритмическом языке вспомогательные алгоритмы оформляются в виде процедур. Запишем на АЯ процедуру СТЕПЕНЬ.
Заголовок вспомогательного алгоритма начинается со слова «процедура», после которого следует имя процедуры и в скобках — список формальных параметров. В этом списке перечисляются переменные-аргументы и переменные-результаты с указанием их типов. Здесь а и k — формальные параметры-аргументы, z — параметр-результат. Следовательно, процедура степень производит вычисления по формуле z = аk. В основном алгоритме «Степенная функция» обращение к процедуре производится путем указания ее имени с последующим в скобках списком фактических параметров. Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия: • по количеству (сколько формальных, столько и фактических параметров); • по последовательности (первому формальному соответствует первый фактический параметр, второму — второй и т.д.); • по типам (типы соответствующих формальных и фактических параметров должны совпадать). Фактические параметры-аргументы могут быть выражениями соответствующего типа. Обращение к процедуре инициирует следующие действия: 1. Значения параметров-аргументов присваиваются соответствующим формальным параметрам. 2. Выполняется тело процедуры (команды внутри процедуры). 3. Значение результата передается соответствующему фактическому параметру, и происходит переход к выполнению следующей команды основного алгоритма. В процедуре степень нет команд ввода исходных данных и вывода результатов. Здесь присваивание начальных значений аргументам (а, п) производится через передачу параметров-аргументов. А присваивание результата переменной (у) происходит через передачу параметра-результата (z). Таким образом, передача значений параметров процедур — это третий способ присваивания (наряду с командой присваивания и командой ввода). Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации. Упражнения 1. Даны декартовы координаты трех вершин треугольника на плоскости. Составить алгоритм определения площади треугольника. 2. Дана скорость ракеты при выходе за пределы атмосферы Земли. Составить алгоритм определения того, как будет двигаться ракета после выключения двигателей. (Напомним величины трех космических скоростей: 7,5 км/с; 11,2 км/с; 16,4 км/с.) 3. Даны три положительных числа. Составить алгоритм, определяющий, могут ли они быть длинами сторон треугольника. 4. Пусть компьютер способен выполнять только две арифметические операции — сложение и вычитание. Составить алгоритмы: а) умножения двух целых чисел; б) целочисленного деления двух чисел; в) получения остатка от целочисленного деления двух чисел. 5. Построить алгоритм решения биквадратного уравнения, используя как вспомогательный алгоритм решения квадратного уравнения. 6. Составить алгоритм нахождения НОД трех натуральных чисел, используя вспомогательный алгоритм нахождения НОД двух чисел.
|

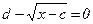 ) то
) то

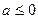 или
или 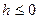 – задача не имеет решения, так как такой треугольник не существует – это частный случай.
– задача не имеет решения, так как такой треугольник не существует – это частный случай.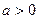 и
и 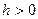 ) -
) - 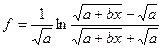
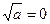 - если знаменатель равен 0
- если знаменатель равен 0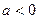 - под корнем отрицательное число
- под корнем отрицательное число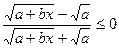 - вычисление логарифма от отрицательного числа или 0
- вычисление логарифма от отрицательного числа или 0 - если знаменатель равен 0
- если знаменатель равен 0 - под корнем отрицательное число
- под корнем отрицательное число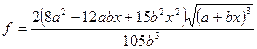

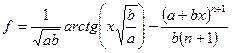


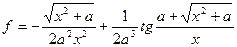
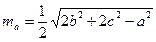
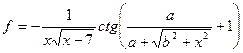
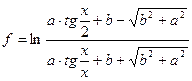
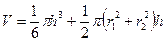 , где r1 и r2 - радиусы основание шарового слоя, h - высота.
, где r1 и r2 - радиусы основание шарового слоя, h - высота.
 .
.