Рекурсивные методы (2)

Суть рекурсивных методов — сведение задачи к самой себе. Вы уже знаете, что как в Паскале, так и в Си существует возможность рекурсивного определения функций и процедур. Эта возможность представляет собой способ программной реализации рекурсивных алгоритмов. Однако увидеть рекурсивный путь решения задачи (рекурсивный алгоритм) часто очень непросто.

Рассмотрим классическую задачу, известную в литературе под названием «Ханойская башня» (рис. 50).

 

На площадке (назовем ее А) находится пирамида, составленная из дисков уменьшающегося от основания к вершине размера.

Эту пирамиду в том же виде требуется переместить на площадку В. При выполнении этой работы необходимо соблюдать следующие ограничения:

• перекладывать можно только по одному диску, взятому сверху пирамиды;

• класть диск можно либо только на основание площадки, либо на диск большего размера;

• в качестве вспомогательной можно использовать площадку С.

Название «Ханойская башня» связано с легендой, согласно которой в давние времена монахи одного ханойского храма взялись переместить по этим правилам башню, состоящую из 64 дисков. С завершением их работы наступит конец света. Монахи все еще работают и, надеемся, еще долго будут работать!

Нетрудно решить эту задачу для двух дисков. Обозначая перемещения диска, например, с площадки А на В так: А → В, напишем алгоритм для этого случая

А→С; А→В; С→В.

Всего 3 хода! Для трех дисков алгоритм длиннее:

А→В; А→С; В→С; А→В; С→А; С→В; А→В.

В этом случае уже требуются 7 ходов.

Подсчитать количество ходов (N) для k дисков можно по следующей рекуррентной формуле:

N(1) = 1; N(k) = 2х N(k - 1) + 1.

Например, N(10) = 1023, N(20) = 104857. А вот сколько перемещений нужно сделать ханойским монахам:

N(64) = 18446744073709551615.

Попробуйте прочитать это число.

Теперь составим программу, по которой машина рассчитает алгоритм работы монахов и выведет его для любого значения п (количества дисков). Пусть на площадке А находятся п дисков. Алгоритм решения задачи будет следующим:

1. Если п = 0, то ничего не делать.

2. Если п > 0, то переместить п — 1 диск на С через В;

переместить диск с А на В (А → В)

переместить п — 1 диск с С на В через А.

При выполнении пункта 2 последовательно будем иметь три состояния (рис. 51).

 

Описание алгоритма имеет явно рекурсивный характер

Перемещение n дисков описывается через перемещение п — 1 диска. А где же выход из этой последовательности рекурсивных ссылок алгоритма самого на себя? Он в пункте 1, каким бы ни показалось странным его тривиальное содержание.

А теперь построим программу на Паскале. В ней имеется рекурсивная процедура Напоу, выполнение которой заканчивается только при п = 0. При обращении к процедуре используются фактические имена площадок, заданные их номерами: 1, 2, 3. Поэтому на выходе цепочка перемещений будет описываться в таком виде:

1→2 1→3 2→3 и т.д.

 

Это одна из самых удивительных программ! Попробуйте воcпроизвести ее на машине. Проследите, как изменяется число ходов с ростом п. Для этой цели можете сами добавить в программу счетчик ходов и в конце вывести его значение или печатать ходы с порядковыми номерами.

Тема 3.4. Методы перебора в задачах поиска (4)

В данном разделе мы рассмотрим некоторые задачи, связанные с проблемой поиска информации. Это огромный класс задач, достаточно подробно описанный в классической литературе по программированию (см., например, книги Н.Вирта, Д. Кнута и другие).

Общий смысл задач поиска сводится к следующему: из данной информации, хранящейся в памяти ЭВМ, выбрать нужные сведения, удовлетворяющие определенным условиям (критериям).

Подобные задачи мы уже рассматривали. Например, поиск максимального числа в числовом массиве, поиск нужной записи в файле данных и т. п. Такой поиск осуществляется перебором всех элементов структуры данных и их проверкой на удовлетворение условию поиска. Перебор, при котором просматриваются все элементы структуры, называется полным перебором.

Полный перебор является «лобовым» способом поиска и, очевидно, не всегда самым лучшим.

Рассмотрим пример. В одномерном массиве X заданы координаты п точек, лежащих на вещественной числовой оси. Точки пронумерованы. Их номера соответствуют последовательности в массиве X. Определить номер первой точки, наиболее удаленной от начала координат.

Легко понять, что это знакомая нам задача определения номера наибольшего по модулю элемента массива X. Она решается путем полного перебора следующим образом:

 

Полный перебор элементов одномерного массива производится с помощью одной циклической структуры.

А теперь такая задача: исходные данные — те же, что и в предыдущей; требуется определить пару точек, расстояние между которыми наибольшее.

Применяя метод перебора, эту задачу можно решать так: перебрать все пары точек из Ладанных и определить номера тех, расстояние между которыми наибольшее (наибольший модуль разности координат). Такой полный перебор реализуется через два вложенных цикла:

 

Очевидно, что такое решение задачи нерационально. Здесь каждая пара точек будет просматриваться дважды, например при i = 1, j = 2 и i = 2, j= 1. Для случая п = 100 циклы повторят выполнение 100 х 100 = 10000 раз.

Выполнение программы ускорится, если исключить повторения. Исключить также следует и случай совпадения значений i и j. Тогда число повторений цикла будет равно

. При n = 100 получается 4950.

Для исключения повторений нужно в предыдущей программе изменить начало внутреннего цикла с 1 на i +1. Программа примет вид:

 

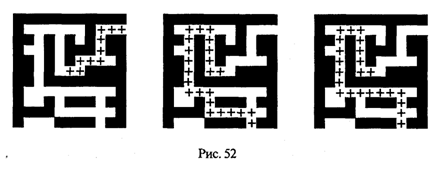
Рассмотренный вариант алгоритма назовем перебором без повторений.

Замечание. Конечно, эту задачу можно было решить и другим способом, но в данном случае нас интересовал именно алгоритм, связанный с перебором. В случае точек, расположенных не на прямой, а на плоскости или в пространстве, поиск альтернативы такому алгоритму становится весьма проблематичным.

В следующей задаче требуется выбрать все тройки чисел без повторений, сумма которых равна десяти, из массива X.

В этом случае алгоритм будет строиться из трех вложенных циклов. Внутренние циклы имеют переменную длину.

For I:=l To N Do

For J:=I+1 To N Do

For K:=J+1 To N Do

If X[I]+X[J]+X[K]=10

Then WriteLn(X[I],X[J],X[K]);

А теперь представьте, что из массива Х требуется выбрать все группы чисел, сумма которых равна десяти. В группах может быть от 1 до п чисел. В этом случае количество вариантов перебора резко возрастает, а сам алгоритм становится нетривиальным.

Казалось бы, ну и что? Машина работает быстро! И все же посчитаем. Число различных групп из п объектов (включая пустую) составляет 2n. При п = 100 это будет 2100 ≈ 1030. Компьютер, работающий со скоростью миллиард операций в секунду, будет осуществлять такой перебор приблизительно 10 лет. Даже исключение перестановочных повторений не сделает такой переборный алгоритм практически осуществимым.

Путь практической разрешимости подобных задач состоит в нахождении способов исключения из перебора бесперспективных с точки зрения условия задачи вариантов. Для некоторых задач это удается сделать с помощью алгоритма, описанного в следующем разделе.

Перебор с возвратом. Рассмотрим алгоритм перебора с возвратом на примере задачи о прохождении лабиринта (рис. 52).

 

Дан лабиринт, оказавшись внутри которого нужно найти выход наружу. Перемещаться можно только в горизонтальном и вертикальном направлениях. На рисунке показаны все варианты путей выхода из центральной точки лабиринта.

Для получения программы решения этой задачи нужно решить две проблемы:

• как организовать данные;

• как построить алгоритм.

Информацию о форме лабиринта будем хранить в квадратной матрице LAB символьного типа размером N x N, где N — нечетное число (чтобы была центральная точка). На профиль лабиринта накладывается сетка так, что в каждой ее ячейке находится либо стена, либо проход.

Матрица отражает заполнение сетки: элементы, соответствующие проходу, равны пробелу, а стене — какому-нибудь символу (например, букве М)

Путь движения по лабиринту будет отмечаться символами +.

Например, приведенный выше рисунок (в середине) соответствует следующему заполнению матрицы LAB:

 

Исходные данные — профиль лабиринта (исходная матрица LAB без крестиков); результат — все возможные траектории выхода из центральной точки лабиринта (для каждого пути выводится матрица LAB с траекторией, отмеченной крестиками).

Алгоритм перебора с возвратом еще называют методом проб.

Суть его в следующем:

1. Из каждой очередной точки траектории просматриваются возможные направления движения в одной и той же последовательности; договоримся, что просмотр будет происходить каждый раз против часовой стрелки — справа-сверху-слева-снизу; шаг производится в первую же обнаруженную свободную соседнюю клетку; клетка, в которую сделан шаг, отмечается крестиком.

2. Если из очередной клетки дальше пути нет (тупик), то следует возврат на один шаг назад и просматриваются еще не испробованные пути движения из этой точки; при возвращении назад покинутая клетка отмечается пробелом.

3. Если очередная клетка, в которую сделан шаг, оказалась на краю лабиринта (на выходе), то на печать выводится найденный путь.

Программу будем строить методом последовательной детализации. Первый этап детализации:

 

Процедура GO пытается сделать шаг в клетку с координатами х, у. Если эта клетка оказывается на выходе из лабиринта, то пройденный путь выводится на печать. Если нет, то в соответствии с установленной выше последовательностью делается шаг в соседнюю клетку. Если клетка тупиковая, то выполняется шаг назад. Из сказанного выше следует, что процедура носит рекурсивный характер.

Запишем сначала общую схему процедуры без детализации:

 

 

Для вывода найденных траекторий составляется процедура PRINTLAB.

В окончательном виде программа будет выглядеть так:

 

 

Еще один пример красивой программы с использованием рекурсивного определения процедуры (вспомните ханойскую башню!).

Схема алгоритма данной программы типична для метода перебора с возвратом. По аналогичным алгоритмам решаются, например, популярные задачи об обходе шахматной доски фигурами или о расстановке фигур на доске так, чтобы они «не били» друг друга; множество задач оптимального выбора (задачи о коммивояжере, об оптимальном строительстве дорог и т.п.).

Замечание. Из-за использования массива LAB в качестве параметра-значения в процедуре GO могут возникнуть проблемы с памятью при реализации программы на ЭВМ. В таком случае можно перейти к глобальной передаче массива.

Упражнения

1. Даны декартовы координаты N точек на плоскости. Составить программы решения следующих задач:

а) найти две самые близкие друг к другу точки;

б) найти две самые удаленные друг от друга точки;

в) найти три точки, лежащие в вершинах треугольника с наибольшим периметром;

г) найти две ближайшие точки, отрезок между которыми может служить радиусом окружности, заключающей внутри себя все остальные точки; указать, какая из них является центральной.

2. Изменить программу Labirint таким образом, чтобы на печать выводился лишь кратчайший путь из центра лабиринта до края.

3. Составить программу, в соответствии с которой шахматный конь обойдет всю доску, побывав на каждом поле всего один раз.

4. Составить программу расстановки на шахматной доске восьми ферзей так, чтобы они не угрожали друг другу.

Тема 3.5. Эвристические методы (2)

Под эвристическими понимаются такие методы, правильность которых строго не доказывается. Они выглядят правдоподобными; кажется, что в большинстве случаев они должны давать верные решения. На уровне экспертной оценки алгоритма часто не удается придумать контрпример, доказывающий ошибочность или неуниверсальность метода. Это, разумеется, не является строгим обоснованием правильности метода. Тем не менее практика использования эвристических методов дает положительные результаты.

Эвристические методы разнообразны, поэтому нельзя описать какую-то общую схему их разработки. Чаще всего они применяются совместно с методами перебора для сокращения числа проверяемых вариантов. Некоторые варианты согласно выбранной эвристике считаются заведомо бесперспективными и не проверяются. Такой подход ускоряет работу алгоритма по сравнению с полным перебором. Платой за это является отсутствие гарантии того, что выбрано правильное или наилучшее из всех возможных решение.

Тема 3.6. Сложность алгоритмов (4)

Традиционно принято оценивать степень сложности алгоритма по объему используемых им основных ресурсов компьютера: процессорного времени и оперативной памяти. В связи с этим вводятся такие понятия, как временная сложность алгоритма и объемная сложность алгоритма.

Параметр временной сложности становится особенно важным для задач, предусматривающих интерактивный режим работы программы, или для задач управления в режиме реального времени. Часто программисту, составляющему программу управления каким-нибудь техническим устройством, приходится искать компромисс между точностью вычислений и временем работы программы. Как правило, повышение точности ведет к увеличению времени.

Объемная сложность программы становится критической, когда объем обрабатываемых данных оказывается на пределе объема оперативной памяти ЭВМ. На современных компьютерах острота этой проблемы снижается благодаря как росту объема ОЗУ, так и эффективному использованию многоуровневой системы запоминающих устройств. Программе оказывается доступной очень большая, практически неограниченная область памяти (виртуальная память). Недостаток основной памяти приводит лишь к некоторому замедлению работы из-за обменов с диском. Используются приемы, позволяющие минимизировать потери времени при таком обмене. Это использование кэш-памяти и аппаратного просмотра команд программы на требуемое число ходов вперед, что позволяет заблаговременно переносить с диска в основную память нужные значения. Исходя из сказанного можно заключить, что минимизация емкостной сложности не является первоочередной задачей. Поэтому в дальнейшем мы будем интересоваться в основном временной сложностью алгоритмов.

Время выполнения программы пропорционально числу исполняемых операций. Разумеется, в размерных единицах времени (секундах) оно зависит еще и от скорости работы процессора (тактовой частоты). Для того чтобы показатель временной сложности алгоритма был инвариантен относительно технических характеристик компьютера, его измеряют в относительных единицах. Обычно временная сложность оценивается числом выполняемых операций.

Как правило, временная сложность алгоритма зависит от исходных данных. Это может быть зависимость как от величины исходных данных, так и от их объема. Если обозначить значение параметра временной сложности алгоритма α символом Tα, а буквой V обозначить некоторый числовой параметр, характеризующий исходные данные, то временную сложность можно представить как функцию Tα(V). Выбор параметра V зависит от решаемой задачи или от вида используемого алгоритма для решения данной задачи.

Пример 1. Оценим временную сложность алгоритма вычисления факториала целого положительного числа.

Function Factorial(x:Integer): Integer;

Var m,i: Integer;

Begin m:=l;

For i:=2 To x Do m:=m*i;

Factorial:=m

End;

Подсчитаем общее число операций, выполняемых программой при данном значении x. Один раз выполняется оператор m:=1; тело цикла (в котором две операции: умножение и присваивание) выполняется х — 1 раз; один раз выполняется присваивание Factorial:=m. Если каждую из операций принять за единицу сложности, то временная сложность всего алгоритма будет 1 + 2 (x — 1) + 1 = 2х Отсюда понятно, что в качестве параметра следует принять значение х. Функция временной сложности получилась следующей:

Tα(V)=2V.

В этом случае можно сказать, что временная сложность зависит линейно от параметра данных — величины аргумента функции факториал.

Пример 2. Вычисление скалярного произведения двух векторов А = (a1, a2, …, ak), В = (b1, b2, …, bk).

АВ:=0;

For i:=l To k Do AB:=AB+A[i]*B[i];

В этой задаче объем входных данных п = 2k. Количество выполняемых операций 1 + 3k = 1 + 3(n/2). Здесь можно взять V= k= п/2. Зависимости сложности алгоритма от значений элементов векторов А и В нет. Как и в предыдущем примере, здесь можно говорить о линейной зависимости временной сложности от параметра данных.

С параметром временной сложности алгоритма обычно связывают две теоретические проблемы. Первая состоит в поиске ответа на вопрос: до какого предела значения временной сложности можно дойти, совершенствуя алгоритм решения задачи? Этот предел зависит от самой задачи и, следовательно, является ее собственной характеристикой.

Вторая проблема связана с классификацией алгоритмов по временной сложности. Функция Tα(V) обычно растет с ростом V. Как быстро она растет? Существуют алгоритмы с линейной зависимостью Тα от V (как это было в рассмотренных нами примерах), с квадратичной зависимостью и с зависимостью более высоких степеней. Такие алгоритмы называются полиномиальными. А существуют алгоритмы, сложность которых растет быстрее любого полинома. Проблема, которую часто решают теоретики — исследователи алгоритмов, заключается в следующем вопросе: возможен ли для данной задачи полиномиальный алгоритм?

Тема 3.7. Методы сортировки данных (2)

Существует традиционное деление алгоритмов на численные и нечисленные. Численные алгоритмы предназначены для математических расчетов: вычисления по формулам, решения уравнений, статистической обработки данных и т.п. В таких алгоритмах основным видом обрабатываемых данных являются числа. Нечиcленные алгоритмы имеют дело с самыми разнообразными видами данных: символьной, графической, мультимедийной информацией. К этой категории относятся многие алгоритмы системного программирования (трансляторы, операционные системы), систем управления базами данных, сетевого программного обеспечения и т.д.

Для программных продуктов второй категории наиболее часто используемыми являются алгоритмы сортировки данных — упорядочения информации по некоторому признаку. От эффективности, прежде всего скорости, их выполнения во многом зависит эффективность работы всей программы.

Различают алгоритмы внутренней сортировки — во внутренней памяти и алгоритмы внешней сортировки — сортировки файлов. Далее мы будем рассматривать только внутреннюю сортировку.

Как правило, сортируемые данные располагаются в массивах. В простейшем случае это числовые массивы. Однако для нечисленных алгоритмов более характерна ситуация, когда сортируется массив записей (в терминологии Паскаля) или массив структур (в терминологии Си). Поле, по значению которого производится сортировка, называется ключом сортировки. Обычно оно имеет числовой тип. Например, массив сортируемых записей содержит два поля: наименование товара и количество товара на складе. В программе на Паскале он описан так:

 

Сортировка производится либо по возрастанию, либо по убыванию значения ключа A[i].key.

Во всех дальнейших примерах программ предполагается, что приведенные выше описания в программе присутствуют глобально и область их действия распространяется на процедуры сортировки. Хотя все примеры приводятся на Паскале, но по тому же принципу можно разработать функции сортировки на Си/Си++.

Здесь мы обсудим два алгоритма: сортировку простым включением и быструю сортировку.

Сортировка простым включением. Предположим, что на некотором этапе работы алгоритма левая часть массива с 1-го по (i — 1)-й элемент включительно является отсортированной, а правая часть с i-го по n-й элемент остается такой, какой она была в первоначальном, неотсортированном массиве. Очередной шаг алгоритма заключается в расширении левой части на один элемент и, соответственно, сокращении правой части. Для этого берется первый элемент правой части (с индексом i) и вставляется на подходящее ему место в левую часть так, чтобы упорядоченность левой части сохранилась.

Процесс начинается с левой части, состоящей из одного элемента А[1], а заканчивается, когда правая часть становится пустой.

 

A-Глобальный массив.

Var i,j,x:Integer:

{20 15 10 7 3}

Begin

For i:=2 To n Do

Begin

x:=A[i];

j:=i-1;

While (x<A[j]) and (j>=1)

Begin

A[j+1]:=A[j]; j:=j-1;

End;

A[j+1]:=x;

End

End;

Теперь оценим сложность алгоритма сортировки простым включением. Очевидно, что временная сложность зависит как от размера сортируемого массива, так и от его исходного состояния в смысле упорядоченности элементов. Временная сложность будет минимальной, если исходный массив уже отсортирован в нужном порядке значений ключа (в данном случае — по возрастанию). Максимальное значение сложности будет соответствовать противоположной упорядоченности исходного массива, т.е. упорядоченности исходного массива по убыванию значений ключа. Обычно для алгоритмов сортировки временная сложность оценивается количеством пересылок элементов.

Оценим величину минимальной временной сложности алгоритма. Если массив уже отсортирован, то тело цикла while не будет выполняться ни разу. Выполнение процедуры сведется к работе следующего цикла:

 

Поскольку тело цикла for исполняется n — 1 раз, то число пересылок элементов массива

Мmin = 2(п - 1),

а число сравнений ключей равно

Сmin = n - 1.

Сложность алгоритма будет максимальной, если исходный массив упорядочен по убыванию. Тогда каждый элемент А[i] будет «прогоняться» к началу массива, т.е. устанавливаться в первую позицию. Цикл while выполнится 1 раз при i = 2, 2 раза при i = 3 и т. д., п — 1 раз при i = п. Таким образом, общее число пересылок записей равно:

 

Более подходящей для реальной ситуации является средняя оценка сложности. Для ее вычисления надо предположить, что все элементы исходного массива — случайные числа и их значения никак не связаны с их номерами. В таком случае результат очередной проверки условия x. key<A[j].key в цикле While также является случайным.

Разумно допустить, что среднее число выполнений цикла While для каждого конкретного значения i равно i/2, т. е. в среднем каждый раз приходится просматривать половину последовательности до тех пор, пока не найдется подходящее место для очередного элемента

Тогда формула для среднего числа пересылок (средняя оценка сложности) будет следующей:

 

Как максимальная, так и средняя оценка сложности алгоритма квадратична (является полиномом второй степени) по параметру п — размеру сортируемого массива.

Алгоритм быстрой сортировки. Этот алгоритм был разработан Э. Хоаром. В алгоритме быстрой сортировки используются три идеи:

• разделение сортируемого массива на 2 части, левую и правую;

• взаимное упорядочение двух частей (подмассивов) так, чтобы все элементы левой части не превосходили элементов правой части;

• рекурсия, при которой подмассив упорядочивается точно таким же способом, как и весь массив.

Для разделения массива на две части нужно выбрать некоторое «барьерное» значение ключа. Это значение должно удовлетворять единственному условию: лежать в диапазоне значений для данного массива (т.е. между минимальной и максимальной величиной). За «барьер» можно выбрать значение ключа любого элемента массива, например первого, или последнего, или находящегося в середине.

Далее нужно сделать так, чтобы в левом подмассиве оказались все элементы с ключом, меньшим барьера, а в правом — с большим: для этого, просматривая массив слева направо, необходимо найти позицию первого элемента с ключом, большим барьера, а просматривая справа налево — найти первый элемент с ключом, меньшим барьера. Следует поменять эти значения, затем продолжить встречное движение до следующей пары элементов, предназначенных для обмена. Необходимо повторять эту процедуру, пока индексы левого и правого просмотров не совпадут. Место совпадения станет границей между двумя взаимно упорядоченными подмассивами. Далее алгоритм рекурсивно применяется к каждому из подмассивов (левому и правому). В конечном счете приходим к совокупности из п взаимно упорядоченных одноэлементных массивов, которые делить дальше невозможно. Эта совокупность образует один полностью упорядоченный массив. Сортировка завершена!

 

 

 

Сложность алгоритма быстрой сортировки. Исследование временной сложности алгоритма быстрой сортировки является очень трудоемкой задачей, и поэтому мы здесь приводить его не будем. Рассмотрим лишь окончательный результат этого анализа. Временная сложность T как функция от п — размера массива — по порядку величины выражается следующей формулой:

Т(п) = 0 (n 1n (n)).

Здесь использовано принятое в математике обозначение: O(х) обозначает величину порядка х. Следовательно, временная сложность алгоритма быстрой сортировки есть величина порядка п 1n(n). Эта величина для целых положительных п меньше, чем п2 (вспомним, что алгоритм сортировки простым включением имеет сложность порядка n2). И чем больше значение п, тем эта разница существеннее. Например: