Системы переключательных функций
В алгебре логики важную роль играет теорема Жегалкина. Теорема Жегалкина. Любая булева функция может быть представлена многочленом следующего вида:
где Теорема Жегалкина даёт возможность представлять любую функцию алгебры логики в виде полиномов различной степени. Существует несколько классов ФАЛ, которые имеют важное значение для логического анализа. 1. Класс константы нуля. К этому классу относятся функции, которые при нулевых значениях аргументов равны 0:
При других значениях аргументов такие функции могут принимать любые значения. 2. Класс константы единицы. К этому классу относятся функции, которые при значениях всех аргументов, равных 1, принимают значение 1:
При других значениях аргументов такие функции могут принимать любые значения. 3. Класс линейных функций. К этому классу относятся функции, которые представимы в следующем виде:
где 4. Класс самодвойственных функций. К этому классу относятся функции, значение которых при отрицании аргументов изменяется на противоположное:
5. Класс монотонных функций. Функция называется монотонно возрастающей, если где 6. Класс симметрических функций. К этому классу относятся функции, для которых значение не меняется при произвольной перестановке аргументов. Пример. Определить, к каким классам относится функция следующего вида:
Составим таблицу истинности для данной функции:
Данная функция относится к классу константы нуля, так как Данная функция относится к классу константы единицы, так как Проверим, относится ли данная функция к классу линейных функций. Пусть
Определим коэффициенты. C0: f(000) = 0 (определили по таблице истинности). Подставим значения функции и логических переменных в уравнение (*) и в результате получим: С0 Å С10 Å С20 Å С30 = 0 Þ С0 = 0. Аналогично C1: f(100) = 1 0 Å х11 Å С20 Å С30 = 1 Þ С1 = 1. C2: f(010) = 0 0Å С10 Å х21 Å С30 = 0 Þ С2 = 0. C3: f(001) = 1 0 Å С10 Å С20 Å х31 = 1 Þ С3 = 1.
Сравним значения функции Данная функция не относится к классу самодвойственных, так как Данная функция не относится к классу монотонных, так как в таблице истинности этой функции несколько переходов с 0 на 1, и с 1 на 0. Данная функция не относится к классу симметрических функций, так как
Функционально полные системы. Базис Система логических функций {f1, f2…fn) называется функционально полной, если любую логическую функцию f можно представить в аналитической форме через функции этой системы. Совокупность функций, с помощью которых достигается функциональная полнота класса, называется базисом класса функций. Совокупность функций, из которой нельзя удалить никакой функции без потери функциональной полноты класса, называется минимальным базисом функций. Используя метод Петрика [2], получаем 17 минимальных базисов для двух переменных: B1 = {¯} - базис Вебба;
B4 = {®, 0 } – импликативный базис;
B6 = {®, Å };
B10 = { \/, } – дизъюктивный базис Буля; B11 = {®, 1 } – коимпликативный базис; B12 = {~, &, 0 }; B13 = { ~,\/, 0 }; B14 = {Å, &, ~ }; B15 = {Å,\/, ~ }; B16 = {Å, &, 1 } - базис Жегалкина; B17 = {Å,\/, 1 }. Рассмотрим критерий полноты системы функций. Теорема Поста – Яблонского. Для того чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию: 1) не сохраняющую 0; 2) не сохраняющую 1; 3) не являющейся линейной; 4) не являющейся монотонной; 5) не являющейся самодвойственной.
|

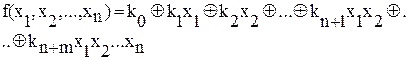 ,
,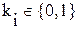 .
.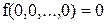 .
. .
.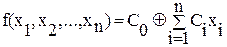 ,
, .
.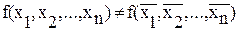 .
.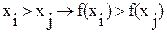 ,
, ,
,  .
. .
.

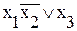
 .
.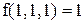 .
.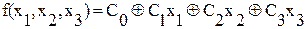 . (*)
. (*)
 и значения исходной функции. Так как значения функций не совпадают, то рассматриваемая функция не относится к классу линейных.
и значения исходной функции. Так как значения функций не совпадают, то рассматриваемая функция не относится к классу линейных. .
.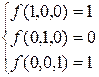 .
. B2 = { ç } - базис Шеффера;
B2 = { ç } - базис Шеффера; B3 = {®, ~ }, где ® - отрицание x1® x2;
B3 = {®, ~ }, где ® - отрицание x1® x2; B7 = {®, } - коимпликативный базис;
B7 = {®, } - коимпликативный базис;



