Аналитическое представление переключательных функций
Номер логического набора. Характеристические функции Номером двоичного набора называется такое десятичное число i, которое получается следующим образом:
где 2 – основание двоичной системы счисления. Например, для логического набора (001) число i примет следующее значение: i = 22*0+21*0+20*1=1. Рассмотрим следующие характеристические функции: 1. Дизъюнктивный терм (макстерм) — это терм, связывающий все переменные, представленные в прямой или инверсной форме, знаком дизъюнкции:
Например, 2. Конъюнктивный терм (минтерм) — это терм, связывающий переменные в прямой или инверсной форме знаком конъюнкции:
Например, F1 = x1x2x3. Рангом терма называется количество переменных, образующих данный терм. Числовое представление ФАЛ Часто для упрощения записи ФАЛ, вместо полного перечисления термов, используют номера наборов, на которых функция принимает значения 0 или 1. Такую форму записи называют числовой. Пример Функцию, заданную следующей таблицей истинности
в числовой форме можно представить в следующем виде: f(x1 x2 x3) = \/1 F(1,3,4,6) или f(x1 x2 x3) = &1 Ф(0,2,5,7). Нормальные формы (НФ) представления ФАЛ Теорема 1. Любая таблично заданная ФАЛ, кроме константы нуля, может быть представлена аналитически в следующем виде:
Доказательство: - если на каком–то наборе функция обращается в 1, то вследствие того, что по аксиоме - если ФАЛ представлена в базисе Дизъюнктивная нормальная форма (ДНФ) – это объединение термов, включающих минтермы переменного ранга. Количество всех минтермов, входящих в формулу (1), равно количеству единичных строк в таблице истинности. Например, произвольная ФАЛ в ДНФ будет выглядеть следующим образом: Следствие из теоремы 1. Любая таблично заданная ФАЛ может быть представлена в следующем аналитическом виде:
Такая форма называется полиномиальной нормальной формой (ПНФ, здесь используется базис Теорема 2. Любая таблично заданная ФАЛ, кроме константы единицы, может быть представлена в следующем аналитическом виде:
Такая форма представления ФАЛ называется конъюнктивной нормальной формой (КНФ). Например, КНФ произвольной ФАЛ: Следствие из теоремы 2. Любая таблично заданная ФАЛ, кроме константы 1, может быть представлена в виде
Такая форма представления ФАЛ называется эквивалентной нормальной формой (ЭНФ). Совершенные нормальные формы КНФ, ДНФ, ПНФ и ЭНФ не дают однозначного представления таблично заданной ФАЛ. Поэтому необходимо рассмотреть совершенные нормальные формы. Введем определение логической степени. Логической степенью называется показатель степени ai логической переменной xi, обладающий следующими свойствами:
Теорема 3. Любая ФАЛ, кроме константы 0, может быть представлена в следующем виде:
В результате получаем дизъюнктивную совершенную нормальную форму (ДСНФ). Приведем основные свойства ДСНФ: 1) отсутствие в любом минтерме одинаковых минтермов; 2) отсутствие в любом минтерме одинаковых переменных; 3) отсутствие в любом минтерме переменной вместе с ее инверсией; 4) все минтермы имеют одинаковый максимальный ранг. Рассмотрим алгоритм получения ДСНФ. Алгоритм 2: Шаг 1. Выделить все единичные значения функции. Шаг 2. Записать все возможные минтермы при единичных значениях функции, причем, переменная х i будет без инверсии, если Шаг 3. Все минтермы объединить знаком дизъюнкции. Пример Определить ДСНФ ФАЛ от трёх переменных, принимающей значение 1 на наборах: 0, 1, 5, 7. Составим таблицу истинности:
Таким образом, ДСНФ данной ФАЛ имеет вид
Для получения ПСНФ (полиномиальная совершенная нормальная форма) необходимо в приведенном выше алгоритме на шаге 3 все минтермы объединить знаком неравнозначности. Для нашего примера 2. ПСНФ ФАЛ имеет вид
Теорема 4. Любая ФАЛ, кроме константы 1, может быть представлена в следующем виде:
В результате получаем конъюнктивную совершенную нормальную форму (КСНФ). Приведем основные свойства КСНФ: 1) отсутствие в любом макстерме одинаковых макстермов; 2) отсутствие в любом макстерме одинаковых переменных; 3) отсутствие в любом макстерме переменной вместе с ее инверсией; 4) все макстермы имеют одинаковый максимальный ранг. Рассмотрим алгоритм получения КСНФ. Алгоритм 3: Шаг 1. Выделить все нулевые значения функции. Шаг 2. Записать все возможные макстермы при нулевых значениях функции, причем переменная хi будет без инверсии, если Шаг 3. Все макстермы объединить знаком конъюнкции. Следствие из теоремы 4. Любая ФАЛ, кроме константы 1, может быть представлена в следующем виде:
Такая форма представления ФАЛ называется эквивалентной совершенную нормальной формой (ЭСНФ). Она получается по алгоритму КСНФ заменой знака конъюнкции на эквивалентность. Пример Определить КСНФ, ЭСНФ ФАЛ от трёх переменных, принимающей значение 0 на наборах: 2, 3, 4, 6. Составим таблицу истинности данной функции:
Таким образом, КСНФ для данной ФАЛ имеет следующий вид:
ЭСНФ данной ФАЛ имеет следующий вид:
Способы преобразования НФ в СНФ Совершенная нормальная форма отличается от НФ тем, что всегда содержит термы только максимального ранга и дает однозначное представление логической функции. Рассмотрим варианты перехода от НФ к СНФ. 1. Преобразование ДНФ к ДСНФ производится по следующей схеме:
Пример Логическую функцию, заданную в ДНФ f(x1,x2,x3) = Решение: обозначим F1 = F’1 = F1 В F2 отсутствует переменная x2, тогда необходимо выполнить следующее преобразование: F’2 = F2 В результате получим: f(x1,x2,x3) = 2. Преобразование КНФ к КСНФ производится следующим образом. Пусть fКНФ = Ф1, тогда fКСНФ = Ф1 \/ Пример Логическую функцию, заданную в КНФ f(x1,x2,x3) = Решение: обозначим Ф1 = Ф’1= Ф1 \/ В результате получаем: f(x1,x2,x3) = (
|

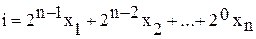 ,
,
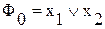 или
или  .
.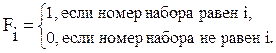


 . (1)
. (1) , то в правой части (6.1)найдётся обязательно элемент, равный 1. Если же на i-м наборе функция обращается в 0, то все элементы нулевые. Таким образом, каждому набору i, для которого функция обращается в 1, соответствует терм, равный 1. А на наборе i, при котором функция обращается в 0, нет ни одного терма, равного 1. Поэтому любая таблица истинности однозначно изображается записью приведенного вида, которая называется объединением термов;
, то в правой части (6.1)найдётся обязательно элемент, равный 1. Если же на i-м наборе функция обращается в 0, то все элементы нулевые. Таким образом, каждому набору i, для которого функция обращается в 1, соответствует терм, равный 1. А на наборе i, при котором функция обращается в 0, нет ни одного терма, равного 1. Поэтому любая таблица истинности однозначно изображается записью приведенного вида, которая называется объединением термов; , то такая форма представления называется нормальной.
, то такая форма представления называется нормальной.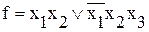 .
.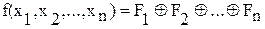 . (2)
. (2)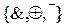 ).
).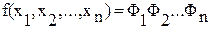 . (3)
. (3)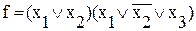 .
. . (4)
. (4)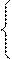 xi, если ai = 1,
xi, если ai = 1, =
=  , если ai = 0.
, если ai = 0.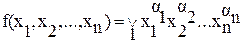 . (5)
. (5) , и с инверсией, если
, и с инверсией, если  .
.

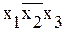



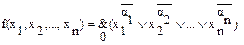 . (6)
. (6) , и с инверсией, если
, и с инверсией, если  .
. . (7)
. (7)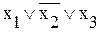
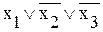

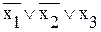
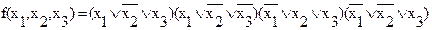
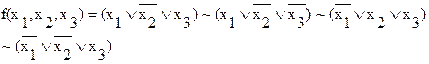
 Пусть fДНФ = F1, тогда f ДСНФ = F1xi \/ F1xi, где xi - переменная, которая не входит в данный терм F1.
Пусть fДНФ = F1, тогда f ДСНФ = F1xi \/ F1xi, где xi - переменная, которая не входит в данный терм F1.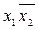 \/
\/  , преобразовать в ДСНФ.
, преобразовать в ДСНФ.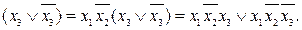
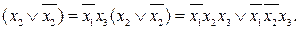

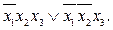
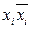 = (Ф1 \/ xi) (Ф1 \/
= (Ф1 \/ xi) (Ф1 \/ 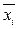 ), где xi – переменная, которая не входит в данный терм Ф1.
), где xi – переменная, которая не входит в данный терм Ф1. , преобразовать в КСНФ.
, преобразовать в КСНФ. . В макстерме Ф1 отсутствует переменная х3, таким образом, необходимо выполнить следующее преобразование:
. В макстерме Ф1 отсутствует переменная х3, таким образом, необходимо выполнить следующее преобразование: = (
= (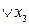 )(
)(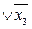 ).
).


