Минимизация переключательных функций
Постановка задачи минимизации ФАЛ Рассмотрим следующее определение. Две ФАЛ называются эквивалентными, если они на одинаковых логических наборах принимают одинаковые значения, т. е. их таблицы истинности совпадают. Совершенно нормальные формы хотя и дают однозначные представления функции, но являются очень громоздкими. Пусть задана логическая функция (которая может представлять собой выход логической схемы или функции переключателей). Каким будет наиболее простое эквивалентное выражение? Для вопросов конструирования цепи переключателей так же, как и для вопросов разработки логических схем, это важные вопросы, поскольку они напрямую связаны с производственными затратами и эффективностью (устойчивостью, помехозащищенностью) работы системы. Все цепи, для которых данная ФАЛ описывает поведение выхода, будут дешевле, если будут содержать меньшее число элементов. Более того, в этом случае будет также меньше вероятность появления ошибок в работе системы. Для заданной ФАЛ более простая ФАЛ, эквивалентная исходной, будет удовлетворять следующим условиях: 1) ни одна другая ФАЛ в такой форме не содержит меньшего числа термов, то есть найденное является наименьшим по числу термов; 2) для всех эквивалентных ФАЛ в такой форме, которые имеют такое же число термов, ни одна не имеет меньшего числа логических переменных в терме (каждая логическая переменная учитывается каждый раз, как только появляется). Если ФАЛ удовлетворяет этим критериям, то такое выражение называется минимальной формой. Преобразование логических функций с целью упрощения их аналитического представления называется минимизацией. Существует два направления минимизации: 1. Сокращение длины ДНФ, КНФ или ПНФ, т. е. уменьшение числа термов в составе функции, эквивалентной данной. При этом получаются кратчайшие функции: КДНФ, ККНФ, КПНФ. 2. Сокращение числа символов Рассмотрим различные методы минимизации. Метод непосредственных преобразований логических функций При применении данного метода записывается ДСНФ логических функций. Затем эта форма преобразуется и упрощается с использованием аксиом алгебры логики. При этом, в частности, выявляются в исходной ДСНФ так называемые соседние минтермы, в которых имеется по одной не совпадающей переменной. По отношению к соседним минтермам применяется закон склейки, в результате чего ранг минтерма понижается на единицу. Например, Минтермы, образованные в результате склеивания, называются импликантами. Полученные после склейки импликанты по возможности склеивают до тех пор, пока склеивание становится невозможным. Несклеивающиеся импликанты называются простыми. Формула, состоящая из простых импликант – тупиковая. Пример
Если в процессе склейки образуется форма R, содержащая члены вида ахi и
Метод неопределенных коэффициентов (МНК) МНК позволяет преобразовывать ДСНФ в МДНФ. На основании теоремы Жегалкина [8], любую ФАЛ можно представить в виде (рассмотрим на примере трех переменных):
Рассмотрим алгоритм определения коэффициентов. Алгоритм 4: Шаг 1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности. Шаг 2. Напротив каждого уравнения поставить соответствующее значение функции. Шаг 3. Выбрать очередную строку, в которой значение функции Шаг 4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках. Шаг 5. Проанализировать оставшиеся коэффициенты в единичных строках. Используя правило, что дизъюнкция равна 1,если хотя бы один из Шаг 6. Записать искомый вид функции. Приведенный алгоритм метода неопределенных коэффициентов применим для дизъюнктивной формы и непригоден для конъюнктивной. Пример Используя МНК, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:0, 2, 4, 7. Составим систему уравнений, записав ее в виде следующей таблицы:
В таблице отмечены те коэффициенты, которые не встречаются в 0 строках. В результате получаем следующую систему уравнений:
В результате определения минимального покрытия имеем следующую МДНФ исходной ФАЛ:
|

 по сравнению с данной ДНФ, которые используются при записи функции в целом. При этом возникают минимальные функции: МДНФ, МКНФ, МПНФ.
по сравнению с данной ДНФ, которые используются при записи функции в целом. При этом возникают минимальные функции: МДНФ, МКНФ, МПНФ.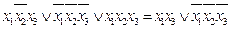 .
.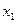


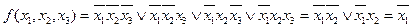
 , то для нее справедливо выражение
, то для нее справедливо выражение  . Это позволяет добавить к исходной форме R несколько членов вида пар ахi и
. Это позволяет добавить к исходной форме R несколько членов вида пар ахi и  , после этого продолжить минимизацию.
, после этого продолжить минимизацию.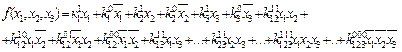
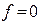 и приравнять все
и приравнять все  к нулю.
к нулю. , выбрать минтермы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.
, выбрать минтермы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.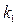
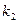






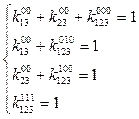
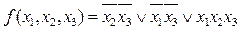 .
.


