Методы минимизации переключательных функций
Метод Квайна. Задача минимизации ФАЛ по методу Квайна состоит в попарном сравнении импликант, входящих в ДСНФ, с целью выявления возможности склеивания по какой-либо переменной по следующему правилу: Таким образом, удается понизить ранг термов. Процедура производится до тех пор, пока не остается ни одного терма, допускающего склейки с другим. Причем склеивающиеся термы помечаются знаком «*». Непомеченные термы называются первичными импликантами. Полученное логическое выражение не всегда оказывается минимальным, поэтому исследуется возможность дальнейшего упрощения. Для этого составляется таблица, в строках которой пишутся найденные первичные импликанты, а в столбцах указываются термы первичной ФАЛ. Клетки этой таблицы отмечаются в том случае, если первичная импликанта входит в состав какого-нибудь первичного терма. Задача упрощения сводится к нахождению такого минимального количества импликант, которые покрывают все столбцы. Рассмотрим алгоритм метода Квайна. Алгоритм 5: Шаг 1. Нахождение первичных импликант. Исходные термы из ДСНФ записывают в столбик и склеивают сверху вниз. Непомеченные импликанты переходят в аналитический вид функции на этом шаге. Процесс склеивания производится, пока это возможно. Шаг 2. Расстановка меток избыточности. Составляют таблицу, в которой число строк равно числу полученных первичных импликант, а число столбцов – числу исходных минтермов. Строки именуют первичные импликанты, а столбцы – минтермы. Если некоторый минтерм содержит первичный импликант, то на пересечении строки и столбца ставят метку. Шаг 3. Нахождение существенных импликант. Если в каком-либо столбце есть только одна метка, то первичный импликант соответствующей строки является существенным, так как без него не будет получено все множество заданных минтермов. Существенные импликанты переходят в аналитический вид функции, а столбцы и строки, соответствующие существенным импликантам, из таблицы вычеркиваются. Шаг 4. Вычеркивание лишних строк. Если в результате вычеркивания столбцов появятся строки первичных импликант, которые не содержат метки или содержат одинаковые метки в строках, то такие первичные импликанты вычеркиваются (кроме одной – меньшего ранга). Шаг 5. Выбор минимального покрытия. Из таблицы, полученной на шаге 3, выбирают такую совокупность первичных импликант, которая включает метки во всех столбцах, по крайней мере, по одной метке в каждом. При нескольких возможных вариантах отдается предпочтение покрытию с минимальным суммарным числом элементов в импликантах, образующих покрытие. Шаг 6. Далее результат записывается в виде функции. Пример Используя метод Квайна, необходимо найти МДНФ функции f(x1,x2,x3,х4), принимающей значение 1 на наборах: 3, 4, 5, 7, 9, 11, 12, 13. Будем решать данную задачу согласно алгоритму 5. Шаг 1. Выпишем минтермы и, используя правило склеивания, будем понижать их ранг.
Шаги 2-4. Составим таблицу, расставим метки, определим существенные импликанты, вычеркнем соответствующие столбцы и строки.
Шаг 5. Выбираем те минтермы, при записи которых, МДНФ функции минимальна. Шаг 6.
Метод Квайна – Мак - Класки Недостаток метода Квайна – необходимость полного попарного сравнения всех минтермов на этапе нахождения первичных импликант. Идея модификации метода Квайна: 1. Каждая конъюнкция в ДСНФ представляется своим двоичным номером набора. 2. Вся совокупность номеров наборов разбивается на группы в зависимости от числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа и т. д.). 3. Сравниваются только две группы, отличающиеся на одну единицу. 4. В результате сравнения в номере набора, имеющего большее число единиц на позиции, где обнаружится разница на одну единицу, ставится прочерк. 5. В процессе преобразования возникают новые сочетания (n-группы). 6. Процесс преобразования длится до тех пор, пока возможна операция склеивания. 7. Элементы преобразованных групп являются первичными импликантами, которые вместе с номерами исходных наборов образуют таблицы разметок. 8. В остальном эти методы совпадают, с единственным уточнением: если в результате таблицы разметок ни одна из строк не покрывает единицу столбца, то надо выбрать номер столбца набора из предыдущей группы преобразований. Пример Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции f(x1,x2,x3,х4), принимающей значение 1 на наборах: 0,1,2,3,4,5,6,7,8,9,11,15. Составим таблицу истинности:
Запишем n-группы: 0- группа: 0000 1- группа: 0001, 0010, 0100, 1000 2- группа: 0011, 0101, 0110, 1001 3- группа: 0111,1011 4- группа: 1111 Теперь сравним группы с номерами i и i+1, в результате чего получим: 0- группа: 000-, 00-0, 0-00, -000 1- группа: 00-1, 0-01, -001, 001-, 0-10, 010-,01-0, 100- 2- группа: 0-11, -011, 01-1, 011-, 10-1 3- группа: -111, 1-11 Еще раз сравним (при этом прочерки должны быть на одинаковых позициях): 0- группа: 00--, 0-0-, -00-, 0--0 1- группа: 0--1, -0-1, 0-1-, 01- - 2- группа: - -11 И еще раз сравним: 0- группа: 0- - - Составим таблицу и найдем покрытие:
Выделим минимальное число импликант из предыдущего шага, покрывающих минтермы, в столбцах которых нет меток. Поскольку не все минтермы покрыты импликантами, достроим таблицу следующим образом:
В результате получаем: fМДНФ(x1 x2 x3 x4) =
Метод диаграмм Вейча (карт Карно) Одним из способов графического представления булевых функций от небольшого числа переменных являются карты Карно. Их разновидность – диаграммы Вейча, которые строятся как развертки кубов на плоскости, при этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется также как таблица истинности. Для ДСНФ единицы ставятся в клетке, соответствующей номеру набора, на котором значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот. Диаграмма для двух логических переменных (для ДСНФ) выглядит следующим образом:
Диаграмма для трех переменных (для ДСНФ):
Диаграмма для четырех переменных (ДСНФ):
x2 110012 111014 01106 01004 x4 x2 110113 111115 01117 01015 x4
Карты (диаграммы) Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации заключается в следующем: склеиванию подвергаются 2,4,8,16,…, При числе переменных 5 и больше отобразить графически функцию в виде единой плоской карты невозможно. Тогда строят комбинированные карты, состоящие из совокупности более простых карт. Процедура минимизации заключается тогда в том, что сначала находится минимальная форма 4-х мерных кубов (карт), а затем, расширяя понятие соседних клеток, отыскивают min-термы для совокупности карт. Причем соседними клетками являются клетки, совпадающие при совмещении карт поворотом вокруг общего ребра. При получении минимальной формы для КСНФ функция задается термами, принимающими нулевое значение на соответствующих наборах. Поэтому в клетках карты пишут нули. Ниже приведен пример карты для двух логических переменных:
x1 x1 \/ x2 x1 \/ x2 Пример Используя метод карт Карно, минимизировать ФАЛ от двух переменных:
Ответ: Пример Используя метод карт Карно, минимизировать следующую ФАЛ:
Замечание Метод неопределенных коэффициентов, метод Квайна – Мак-Класки применимы для минимизации функций, заданных в различных базисах (например, {Å, /\,
Вопросы для самопроверки
|

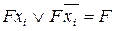 .
.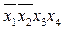 * 1
* 1
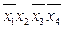 * 3
* 3
 * 4
* 4
 * 1
* 1
 * 2
* 2
 * 2
* 2
 * 3
* 3
 * 4
* 4
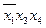

 * 1
* 1
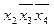 * 2
* 2

 * 2
* 2

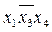
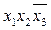 * 1
* 1
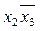
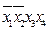

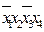
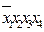

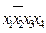
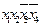
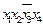








 V
V
 V
V
 .
.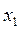

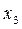


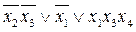 .
.

 x1 x1
x1 x1 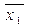

 x2 10019 101111 00113 00011 x4
x2 10019 101111 00113 00011 x4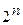 соседних клеток и клетки, лежащие на границе карты.
соседних клеток и клетки, лежащие на границе карты. x2 x2
x2 x2
 .
.



 .
. .
.



 1
1


 },{|}, {¯}) [8].
},{|}, {¯}) [8].


