Параметрические и непараметрические критерии
Статистические критерии, с помощью которых можно установить достоверность различия между параметрами (M, σ;) вариационных рядов одноимённого признака в двух выборках (или в выборке и генеральной совокупности) называются параметрическими. Они используются при предположении, что распределения сравниваемых рядов близки к нормальному. Критерий Стьюдента (t). Весьма известный критерий, предложенный У. Госсетом. Критерий Стьюдента для сравнения одноимённых параметров (P1 и P2) двух вариационных рядов имеет при n>20 в общей форме вид:
где в знаменателе стоит ошибка разности этих параметров, представляющая собою корень квадратный из суммы квадратов ошибок репрезентативности выборочных параметров:
С учётом формул ошибок репрезентативности критерий t приобретает окончательный вид: § для сравнения средних арифметических:
§ для сравнения средних квадратических отклонений:
Оценка достоверности разницы производится с помощью сравнения полученного значения t со стандартным (tst), взятым из соответствующей таблицы при выбранном уровне достоверности и числе степеней свободы. Рассмотрим пример: Изучалось число лепестков венчика у Ficaria verna из двух популяций в окрестностях г. Пушкина Ленинградской области (1965 г.). Были получены следующие выборочные параметры:
Критерий t для определения достоверности разницы между средними:
Критерий t для определения достоверности разницы между средними квадратичными отклонениями:
По таблице значений tst при
Критерий Фишера (F) является более точным критерием сравнения средних квадратических отклонений. Он представляет собой отношение двух дисперсий:
причём в числителе берут большую дисперсию их двух. Для вышерассмотренного примера имеем:
Из таблицы стандартных критериев Фишера находим, при Для сравнения двух выборок, распределение которых далеко от нормального или выборки весьма малы, рекомендуется использовать непараметрические критерии различия. Рассмотрим некоторые из них, которые активно применяются в биологических науках (в частности в экологических исследованиях). Критерий χ-квадрат. Критерий был открыт ещё в 1875-1877 гг. Хельмертом, но затем был забыт и открыт уже К. Пирсоном. Рассчитывается по формуле:
где f – наблюдаемая частота; f* - ожидаемая частота. § Если χ2 > χ2st. То нулевая гипотеза об отсутствии различия между теоретическим и эмпирическим распределениями отвергается. § Если χ2 < χ2st. То нулевая гипотеза об отсутствии различия между теоретическим и эмпирическим распределениями принимается. Число степеней свободы находится по формуле: Рассмотрим пример: Проверим гипотезу об отсутствии относительной приуроченности вида к какому-либо местообитанию на примере пчелы Megachile rotundata (F.) по 7-летним материалам. М = 5; N = 22905; Ожидаемое число особей рассчитываем по формуле:
где Nj – число особей S видов в j -ой выборке.
Таблица 2.1
|

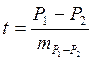 ,
,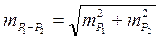 .
.
 .
.
 .
.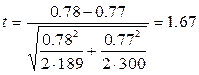 .
.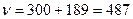 (почти 500) t01=2.59. Делаем вывод: две популяции Ficaria verna достоверно отличаясь по среднему признака совпадают по степени изменчивости числа лепестков.
(почти 500) t01=2.59. Делаем вывод: две популяции Ficaria verna достоверно отличаясь по среднему признака совпадают по степени изменчивости числа лепестков. ,
, .
. и
и 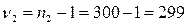 . Берём близкие значения по таблице:
. Берём близкие значения по таблице:  и
и 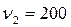 . При 1%-ом уровне достоверности получаем F=1.39. Видим, что F < Fst и следовательно вывод совпадает с предыдущим.
. При 1%-ом уровне достоверности получаем F=1.39. Видим, что F < Fst и следовательно вывод совпадает с предыдущим. ,
, , где М – число классов.
, где М – число классов.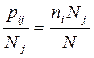 ,
,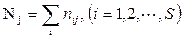 , а ni – общее число особей одного вида во всех выборках М;
, а ni – общее число особей одного вида во всех выборках М; 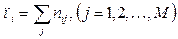 , а pij – доля i -го вида в j -ой выборке.
, а pij – доля i -го вида в j -ой выборке.


