Матрица наблюдений однофакторного дисперсионного комплекса
Средние этих выборок обозначим через Гипотеза Н0 проверяется сравнением внутригрупповых и межгрупповых дисперсий по F -критерию. Если расхождение между ними незначительно, то нулевая гипотеза принимается. В противном случае нулевая гипотеза отвергается и делается заключение о том, что различия в средних обусловлено не только случайностями выборок, но и действием исследуемого фактора. Для изучаемого признака характерно три типа изменчивости: 1. Факториальная (или групповая) изменчивость. Характеризуется тем, что для каждой из совокупностей имеется своя средняя арифметическая ( 2. Остаточная изменчивость. Характеризуется различными значениями признака внутри каждой градации. Эти различия не зависят от влияния фактора. Видимо, их причина лежит вне опыта, определяется неучитываемыми в данном анализе факторами. 3. Общая изменчивость. Заключается в том, что все наблюдения дисперсионного комплекса отличаются друг от друга (или иногда совпадают). Мерой изменчивости признака в выборке служит сумма квадратов отклонений его значений от средней арифметической 1. Мерой факториальной изменчивости будет сумма квадратов отклонений средних значений групп ( 2. Мера остаточной изменчивости выразится суммой квадратов отклонений всех наблюдений в данной совокупности от среднего значения совокупности: 3. Мерой общей изменчивости является сумма квадратов отклонений в дисперсионном комплексе от общего среднего: Тогда в соответствии с основной идеей дисперсионного анализа можно записать: S2y=S2x+S2z или:
Вычислим факториальную и остаточную дисперсии, как меры соответствующих типов изменчивости признака в дисперсионном комплексе
В этих формулах фигурируют степени свободы (nх, nz, nу), т.к. дисперсия s2 и есть сумма квадратов отклонений в расчете на одну степень свободы. Число степеней свободы есть количество значений, необходимых для восстановления утерянного. 1. Число степеней свободы для факториальной дисперсии равно числу совокупностей без единицы (m -1), т.к. все группы связаны друг с другом лишь одним общим условием – значением средней арифметической всего дисперсионного комплекса ( 2. Число степеней свободы для остаточной дисперсии равно числу наблюдений в комплексе минус число совокупностей (mn-m) ибо все наблюдения связаны наличием в каждой группе своей средней арифметической ( 3. Число степеней свободы для вычисления общей дисперсии всего комплекса равно числу наблюдений в комплексе без единицы (mn- 1), ибо все наблюдения связаны только одним общим условием – наличием общей средней ( Затем необходимо рассчитать доли влияния учтенного и неучтенного факторов как отношения соответствующих сумм квадратов отклонений:
Эти величины представляют собой не что иное, как квадраты корреляционных отношений. В сумме эти показатели должны всегда составлять 1 (100%). Теперь можно ответить на интересующий вопрос: насколько учитываемый фактор ответственен за изменчивость результативного признака и сколько процентов падает на долю неучтенных факторов. Таблица 2.4
|
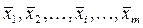. Для проверки гипотезы о равенстве средних нулевую гипотезу запишем как 
, альтернативную в виде 
.
). Разница в средних зависит, очевидно, от разного действия факторов;
. Эта величина, отнесенная к числу наблюдений, дает меру рассеяния, именуемую дисперсией, которая и применяется в дисперсионном анализе.
) от общего среднего 
: 
. Эту величину иногда называют рассеиванием по факторам.
.
.
.
.
).
).
).
.
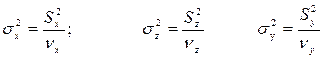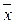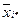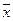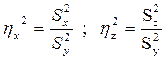