Регрессионный анализ. В экологических исследованиях, и особенно в обработке экспериментальных данных, обычно используется регрессионный анализ

В экологических исследованиях, и особенно в обработке экспериментальных данных, обычно используется регрессионный анализ, который тесно связан с корреляционным анализом и является его логическим продолжением, углубляя представления о корреляционной связи.

Под регрессией подразумевается зависимость изменений одного признака от изменений другого или нескольких признаков (множественная регрессия). В отличие от строгой функциональной зависимости y = f(x) в регрессионной модели одному и тому же значению величины x могут соответствовать несколько значений величины y, иными словами, при фиксированном значении x величина y имеет некоторое случайное распределение. В соответствии с этим регрессия, подобно корреляции, может быть парной (простой) или множественной, а в зависимости от формы связи – линейной или нелинейной. Здесь мы рассмотрим только самый простой случай линейной регрессии.

В случае простого линейного регрессионного анализа целесообразно придерживаться следующей схемы исследования. Пусть имеется две переменные – X (независимая) и Y (зависимая). Случайным образом отбираем n индивидов из генеральной совокупности и измеряем для них обе переменные. Далее строим диаграмму рассеяния признаков. Анализируя её, мы можем эмпирически оценить допустимо ли предположение о линейной зависимости между переменными. При большом числе переменных точки графика образуют «облако» характерной формы.

Рисунок 2.1. Типы диаграмм рассеяния.

 

По форме «облака» можно сделать некоторые выводы (рис. 2.1): А) положительная линейная корреляция (r > 0) (например, связь между ростом и весом); Б) отрицательная линейная корреляция (r < 0) (например, связь между возрастом и весом монеты); В) отсутствие связи (r = 0); Г) отрицательная нелинейная корреляция (r < 0) (например, связь между спросом и ценой на товар).

 

Теперь рассчитываем таблицу коэффициентов корреляции Пирсона. В отличие от корреляционного анализа, требующего достаточно большого объема выборки, анализ регрессии возможен и при наличии всего нескольких пар сопряженных наблюдений, однако его имеет смысл проводить лишь при обнаружении достоверных и достаточно сильных (порядка r ≥ 0,7) связей между признаками.

После того как мы определились с характером связи, строим модель в виде линейной функции:

,

где значения b это некоторый параметр, указывающий на связь двух выборок. Например, b₀ – это значение Y, полученное при X = 0, тогда b₁ – прирост Y при увеличении X на единицу (скорость изменения).

Рассчитываются коэффициенты модели весьма просто:

,

.

Полученные данные подставляем в формулу линейной регрессии и строим график линейной регрессии. Далее требуется оценить степень связности двух линий регрессии – эмпирической и теоретической. Для этих целей оценивают дисперсии. Обычно используют уже вам известную таблицу дисперсионного анализа.

Таблица 2.6

Таблица дисперсионного комплекса для простой линейной регрессии

Компоненты дисперсии	Сумма квадратов	Степени свободы	Средний квадрат	F -отношение
Регрессия
Отклонение от регрессии
Полная (общая)

 

Обусловленная регрессией сумма квадратов SS_D получила своё название потому, что её можно записать как функцию оценённого коэффициента регрессии b₁:

.

Итак, чем больше коэффициент регрессии, тем больше сумма квадратов регрессии, «обусловленная регрессией». F -отношение может быть использовано для проверки гипотез.
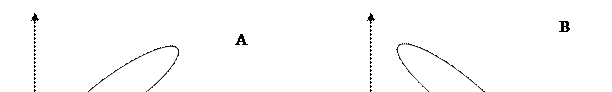
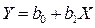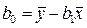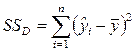
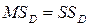
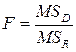
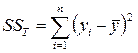
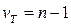