Матрица пересечений гипотетического примера

Напоминаем, что матрица симметрична относительно диагонали. Оцениваем разнородность диагональных элементов. Они одновелики (перепады значений незначительны), следовательно можно применять меры сходства. Для иллюстрации методов сравнительного анализа мы также рассчитаем и матрицу мер включения (как вам уже известно, данная матрица является наиболее информативной относительно степени сходства биологических объектов):

Таблица 3.3

Матрица мер включения гипотетического примера (в %)

В нашем случае наблюдается очень большое сходство между площадками. При пороге в 100% 1 площадка включается в площадки 2-5, 2 площадка в 5 площадку, 3 площадка в 4-5, 4 в 3 и 5. Представьте эти отношения в виде ориентированного графа и оцените банальность/оригинальность видовых списков. Методом симметризации рассчитаем матрицу мер сходства Сёренсена (напомним, что эта матрица является двойственной матрице мер различия (расстояний), т.е. мера сходства является дополнением до единицы матрицы различия).

Таблица 3.4

Матрица мер сходства Сёренсена гипотетического примера (в %)

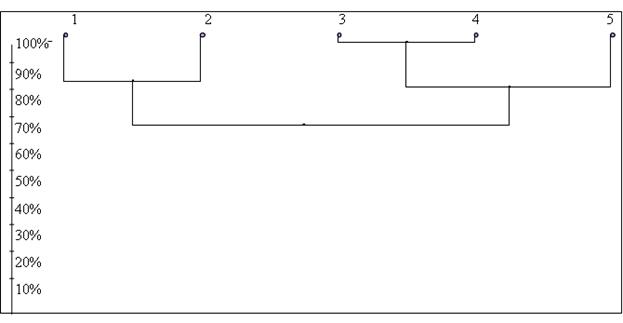
Определим кластеры с помощью метода арифметического среднего (рис 3.1). Для этого просматривая ячейки сверху вниз и слева направо, ищем максимальное значение сходства (кроме диагональных элементов).

Рисунок 3.1. Дендрограмма, построенная методом среднего арифметического связывания (мера сходства Сёренсена).

Находим на пересечении 3 и 4 площадки 100%. Это наш первый кластер [3, 4]. Все значения матрицы, которые пересекаются с элементами нового кластера пересчитываем как среднее арифметическое этих значений. Например, K_1,3=80, K_1,4=80, следовательно среднее арифметическое также будет равно 80 (K_1[3,4]=80). Аналогично определяем следующие кластеры. Рассчитайте самостоятельно и постройте дендрограмму. Последовательно получим: кластер [1, 2] = 87,5; кластер [[3,4],5] = 85,5. Объединение кластеров происходит на уровне сходства – 74%.