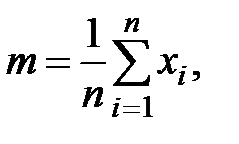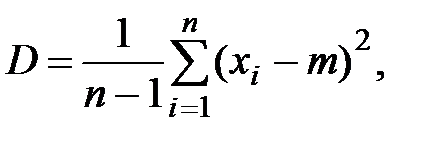ПРАКТИЧЕСКАЯ ЧАСТЬ. Пример 1. Написать программу сортировки по возрастанию заданного массива случайных чисел, равномерно распределенных в интервале [–6; 6]
Пример 1. Написать программу сортировки по возрастанию заданного массива случайных чисел, равномерно распределенных в интервале [–6; 6], с помощью вспомогательной функции. Программный код решения примера
Следует обратить внимание на имена формальных параметров в самой функции sort() и в ее прототипе: они имеют разные имена, но одинаковые типы. Фактические параметры, или аргументы, функции sort() в вызывающей программе (в теле функции main()) имеют свои имена, не связанные с именами формальных параметров. Заполнение массива случайными числами производится с помощью библиотечной функции rand() и макроопределения RAND_MAX.
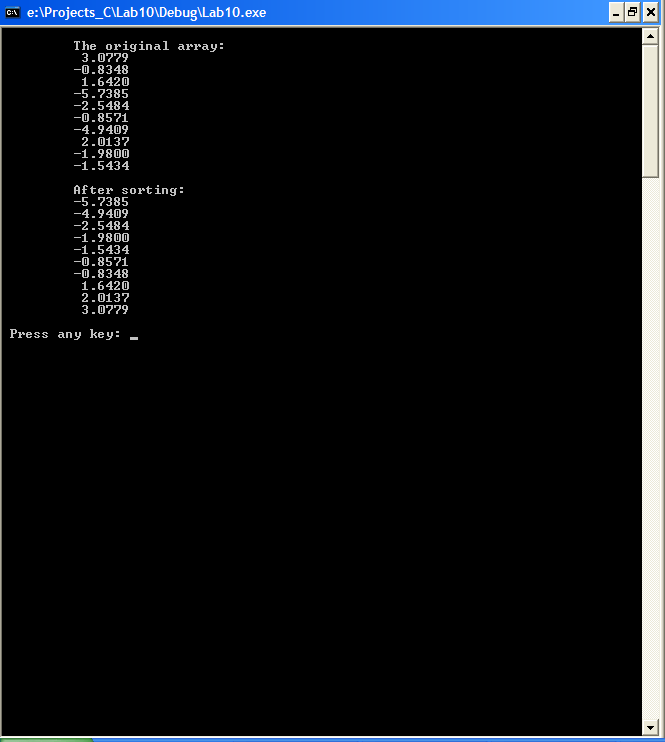
Рис. 10.2. Пример сортировки числового массива Задание 1 1. Используйте программу без прототипа функции sort(). 2. С помощью вспомогательной функции произведите сортировку массива по убыванию. 3. С помощью вспомогательной функции произведите сортировку целых чисел из заданного интервала [X; 10X], где Х – номер компьютера, на котором выполняется лабораторная работа. 4. Создайте функцию умножения исходного массива как матрицы-столбца на отсортированный массив как матрицу-строку. Выведите на консоль результат перемножения. 5. Создайте функцию умножения исходного массива как матрицы-строки на отсортированный массив как матрицу-столбец. Выведите на консоль результат перемножения. Пример 2. Написать программу вычисления квадратного корня числа по методу Ньютона – Рафсона с использованием функции расчета квадратного корня числа и функции расчета абсолютного значения числа. При вычислении квадратного корня из числа следует помнить, что подкоренное выражение не должно быть отрицательным. Алгоритм метода Ньютона – Рафсона для вычисления квадратного корня числа. Шаг 1. Выбрать приблизительное значение 1. Шаг 2. Если | guess 2 – x | < e, перейти к шагу 4 (англ. guess – предположение). Шаг 3. Установить приблизительное значение, равное (x / guess + guess)/2, и перейти к шагу 2. Шаг 4. Считать приблизительное значение квадратным корнем числа [5]. Программный код решения примера
В программе используются три функции: main(), absValue(), squareRoot(). Вспомогательные функции расположены в определенном порядке: сначала absValue(), а потом squareRoot(). В первую передается значение guess, которое вычисляется в функции squareRoot(), находящейся в условии оператора цикла if. Когда условие для оператора цикла будет ложным, т. е. когда значение корня будет меньше заданного числа epsilon, полученное значение возвращается в вызывающую функцию main(). В программе использована переменная epsilon, определенная с помощью спецификатора const, что делает ее неизменной. При таком объявлении компилятор определяет ее как константное значение. Таким переменным нельзя присваивать значения в программе, их нельзя инкрементировать или декрементировать [2].
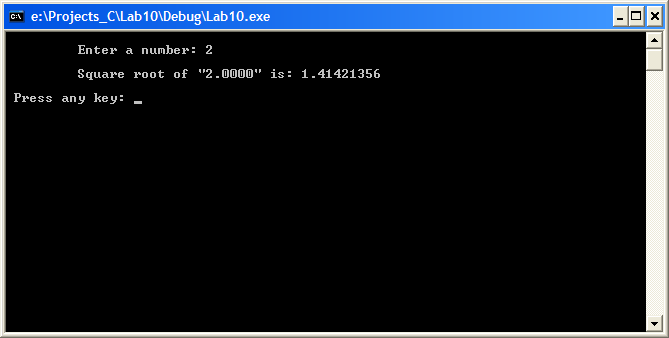
Рис. 10.3. Результат итерационного извлечения квадратного корня из двух Задание 2 1. В функции absValue() примените оператор условия? вместо оператора if без определения дополнительной переменной. 2. В главной функции main() введите проверку ввода неотрицательного числа. 3. В программу введите прототипы функций. 4. Зафиксируйте результат вычисления квадратного корня от числа Х, где Х – номер компьютера, на котором выполняется лабораторная работа. 5. В качестве начального приближения возьмите 1,5Х, где Х – номер компьютера, на котором выполняется лабораторная работа. 6. В программе примените тип float вместо типа double. Пример 3. Написать программу поиска максимального элемента среди минимальных элементов строк двухмерного целочисленного массива. Условие примера соответствует поиску максмина в двухмерном массиве, т. е.
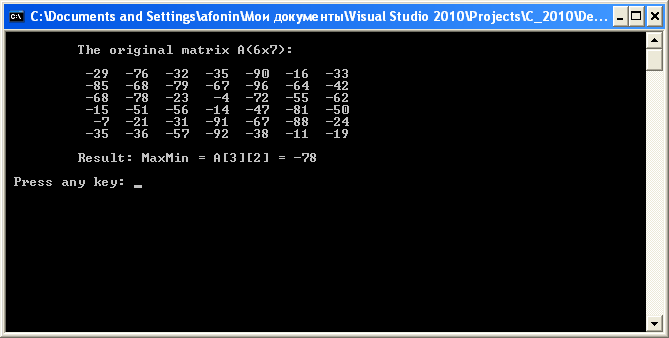
где Алгоритм поиска максмина заключается в следующем [6]. Сначала предполагаем, что максимальным элементом является начальный элемент первой строки A[0][0], затем заменяем его минимальным элементом этой же строки, т. е. теперь минимальный элемент первой строки принимается за искомый максимум. Последовательно просматривая остальные строки, находим в каждой из них минимальный элемент. Если окажется, что минимальный элемент текущей строки больше текущего максимума, то он принимается за максимальный. Результатом поиска являются значение максимального элемента и его индексы (номер строки и номер столбца). Программный код решения примера
Возможный результат выполнения программы представлен на рис. 10.4. Рис. 10.4. Пример вычисления максмина двухмерного массива Задание 3 1. Подсчитайте число итераций, используемых при поиске максмина. 2. В объявлении матрицы MaxMin() (и ее прототипа) примените указатель на одномерный массив, например int *a вместо int A[ ][m]. 3. Число строк матрицы задайте как 3Х, где Х – номер компьютера, на котором выполняется лабораторная работа. 4. Размерность анализируемого массива (матрицы) задайте с клавиатуры. С клавиатуры задайте также интервал генерирования случайных чисел функцией rand() в виде [–2Х; 2Х], где Х – номер компьютера, на котором выполняется лабораторная работа. 5. Напишите функцию определения субмаксмина, т. е. максимального числа среди минимальных чисел строк двухмерного массива после найденного максмина. 6. Определите абсолютные значения максимума и минимума сформированной матрицы, для которой находится максмин. Пример 4. Написать программу поиска одного элемента в линейной неупорядоченной таблице по совпадению ключа на основе заграждающего элемента. Таблицу описать в виде одномерного массива целых чисел [6]. В линейной таблице элементы располагаются друг за другом, т. е. для каждого из них существуют отношения порядка [6]. Линейные таблицы в оперативной памяти компьютера представляются массивами или линейными связанными списками. Поиск одного элемента в неупорядоченной таблице по заданному условию осуществляется последовательным просмотром элементов или до нахождения искомого, т. е. до выполнения условия поиска, или до конца таблицы, если искомый элемент необнаружен. Возвращаемыми значениями являются адрес (индекс) элемента, или значение элемента, либо признак его отсутствия [6]. В случае применения заграждающего элемента последняя запись таблицы запоминается, а после завершения поиска восстанавливается в таблице. В последний элемент массива (когда таблица представляется в виде одномерного массива данных) заносится ключ поиска, и образуется так называемый заграждающий элемент. Теперь на каждом шаге поиска осуществляется только одно сравнение, а сам поиск продолжается до нахождения элемента с заданным ключом. Если искомого элемента в исходной таблице не было, то поиск закончится на заграждающем элементе. Таким образом, его использование при наличии числовых ключей существенно сокращает количество сравнений. Программный код решения примера
В программе использовано внешнее объявление одномерного массива с инициализацией. Термин «внешний» здесь используется, чтобы подчеркнуть расположение объявления вне функций; напрямую с ключевым словом extern он не связан [4].
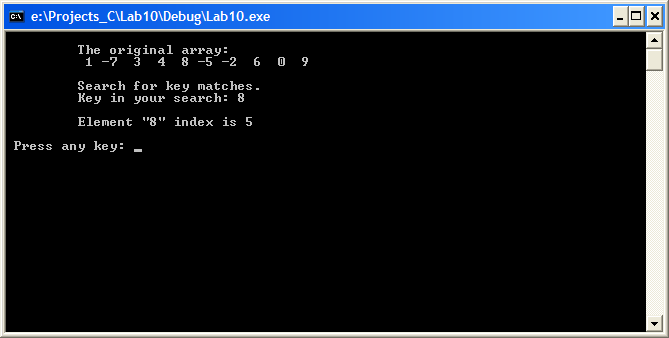
Рис. 10.5. Пример поиска элемента в массиве по заданному ключу Задание 4 1. Подсчитайте число итераций при поиске элемента по заданному ключу. 2. Напишите программу без заграждающего элемента. Подсчитайте число итераций при поиске элемента по заданному ключу. Сравните с числом итераций при поиске с заграждающим элементом. 3. Сформируйте динамический одномерный массив размерностью 12Х, и заполните его целыми случайными числами, распределенными равномерно из интервала [0; 20X], где Х – номер компьютера, на котором выполняется лабораторная работа. Ввод ключа для поиска выполните с клавиатуры. Поиск выполните с заграждающим элементом. 4. С учетом предыдущего пункта задания ввод ключа задайте случайным образом. Если по этому ключу элемент не найден, то программным путем организуйте повторный поиск с заданием нового случайного ключа. В случае если при 5Х-кратном поиске элемент не найден, выведите сообщение об отсутствии искомого элемента по всем заданным ключам. Поиск выполнить с заграждающим элементом. Пример 5. Написать программу выделения слов из символьной строки, когда слова в ней разделены пробелами, и поместить каждое слово в отдельной строке свободного (вспомогательного массива) [6]. Программный код решения примера
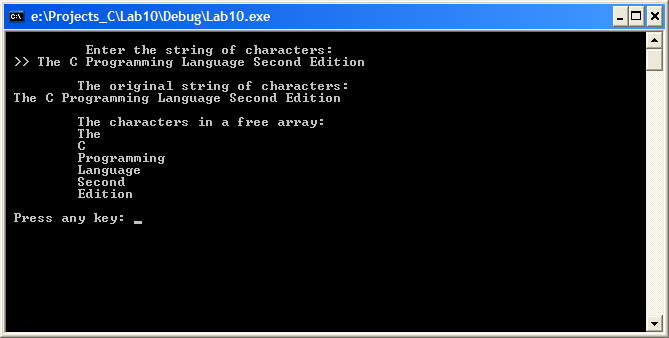
В программе использована библиотечная функция strtok(), которая выделяет слова из строки. При этом для каждого выделенного слова получаем динамическую память с помощью функции calloc(). Адрес выделенной памяти помещаем в соответствующий указатель массива свободных строк FA[]. Обратите внимание, что в функции calloc() вводится число на единицу больше, чем длина строки. Это сделано для учета символа завершения строки (или одного слова) '\0'. Для исключения предупреждений о безопасной работе с функциями strcpy(), strtok() в MS Visual Studio в программе используется директива #define _CRT_SECURE_NO_WARNINGS.
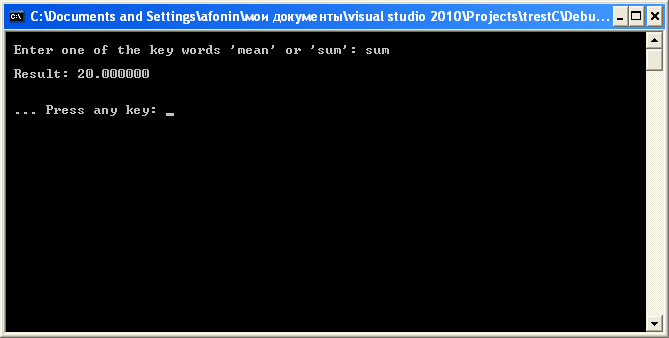
Рис. 10.6. Пример выделения слов из строки Задание 5 1. В программу включите обработку символов: запятая ',', точка с запятой ';' точки '. ' в качестве разделителей слов. 2. Используйте символ пробела для разделения слов «фамилия, имя, год поступления в вуз». 3. В программу включите прототип функции wordstr(). 4. Изучите возможность применения в программе функций strcpy_s() и strtok_s(). Пример 6. Написать программу расчета суммы и среднего арифметического числовых произвольного количества данных. В качестве ключевых слов для выбора варианта расчета принять mean (среднее) и sum (сумма). В данном примере необходимо использоватеь функцию с переменным числом агрументов. Формула расчета среднего арифметического (m):
где n – количество числовых данных, xi – текущее число. Программный код решения примера
Рис. 10.7. Пример выполнения программы Задание 6 1. Напишите функцию с явным указанием количества аргументов. 2. Включите в программу расчет исправленной выборочной дисперсии (D), которая рассчитывается по формуле
где m – среднее арифметическое заданных чисел.
Контрольные вопросы 1. Что лежит в основе всех программ, созданных на языке С? 2. Какие типы данных функция возвращать может и что не может? 3. Что такое прототип функции? Какие элементы объявления функции входят в ее прототип? 4. В чем разница между фактическими и формальными параметрами функции? 5. Какой способ передачи параметров в функциях предусматривает синтаксис языка С? 6. Как можно изменить значение аргумента функции в теле самой функции? 7. Какова область видимости переменных, определенных в теле функции? 8. Можно ли использовать функцию без параметров и без служебного слова void? К каким последствиям это может привести? 9. Какие обязательные атрибуты должна содержать функция с переменным числом аргументов?
|

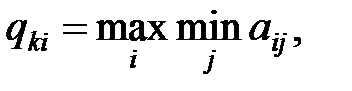
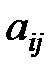 – элементы матрицы А.
– элементы матрицы А.