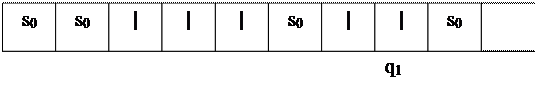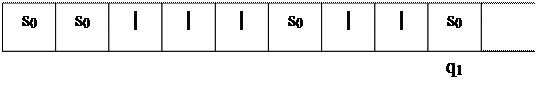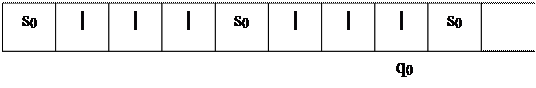Задача 1. Какую работу выполнит машина Тьюринга, если она работает по программе:
Какую работу выполнит машина Тьюринга, если она работает по программе:
Пусть перед началом работы машины ее память (лента) имеет вид
Согласно программе, обозревая ячейку, в которой хранится знак |, и находясь в состоянии q1 машина производит следующее действие: не производя никаких изменений в воспринимаемой ячейке, управляющая головка движется вправо и машина остается в состоянии q1 Состояние ленты после первого такта работы машины будет таким:
Дальнейшее действие приводит к остановке машины с состоянием ленты:
Таким образом, рассматриваемая машина отыскивает первую пустую ячейку справа от воспринимаемой, печатает на ней букву алфавита и останавливается, воспринимая эту ячейку. Условимся представлять числа 0, 1, 2, 3,... словами в алфавите {|}: |, ||, , Соответственно. Для представления на ленте набора целых неотрицательных чисел x1, x2,..., xn мы будем писать соответствующее число раз букву |, оставляя в точности одну пустую ячейку между каждыми двумя словами (конечными последовательностями букв |). Так, набор чисел 3, 0, 2 запишется на ленте следующим образом: s0 | | | | s0 | s0 | | | s0 s0 Учитывая это, работу рассмотренной машины (назовем ее машиной A) можно охарактеризовать следующим образом: машина A, воспринимая последнее число набора чисел (в стандартном положении), увеличивает его на единицу и останавливается, воспринимая полученное число. В дальнейшем мы будем иметь дело только с целыми неотрицательными числами (расширенным нулем множеством натуральных чисел) или наборами этих чисел и их записями в однобуквенном алфавите {|}.
|