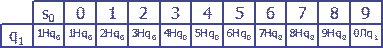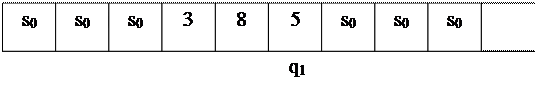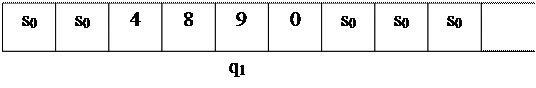Пример. Алфавит этой машины Тьюринга A = {s0, 0, 1,2, 3, 4, 5, 6, 7, 8, 9}, а множество состояний: Q = {q0, q1}
Рассмотрим машину Тьюринга, программа которой задана таблицей 2:
Алфавит этой машины Тьюринга A = {s0, 0, 1,2, 3, 4, 5, 6, 7, 8, 9}, а множество состояний: Q = {q0, q1} Какую задачу решает эта машина? Допустим, что в памяти машины перед началом работы хранится число 385, т. е. лента имеет вид, показанный на таблице 3 а):
Таблица 3 a)
б)
Из таблицы 3 а) видно, что машина в состоянии q1 обозревает самый правый символ записи на ленте. Из программы (таблица 2) следует, что соответствующая паре (5,q1) команда имеет вид: 6Нq0. Согласно этой команде машина стирает цифру 5 в обозреваемой ячейке и помещает в ней цифру 6, остается на месте и переходит в состояние q0, т. е. останавливается, причем состояние памяти будет таким, как показано в таблице 3, б). Таким образом, машина прибавила 1 к исходному числу. Рассмотрим теперь другую начальную ситуацию, показанную на таблице 4 а), т.е. в памяти машины хранится число 4899. Таблица 4 a)
б)
в)
г)
По окончании работы машины лента имеет вид, приведенный на таблице 4, г). Когда исходное число — 4899, машина прибавляет единицу и останавливается. Нетрудно заметить, что вообще машина, определяемая программой, заданной таблицей 2, воспринимая в начальном положении запись любого натурального числа в десятичной системе счисления, по окончании своей работы будет выдавать в качестве результата запись этого числа, увеличенного на 1.
В дальнейшем будем считать, что машина всегда в начальном состоянии (т.е. в состоянии q1) воспринимает самый правый символ записи на ленте (разумеется, отличный от s0), и называть это положение, в котором машина воспринимает запись на ленте, стандартным.
|