Задача 11.
а) Покажите, что операция композиции машин ассоциативна, т.е. для любых машин M1, M2, M3 (M1°М2)°М3 = М1°(М2°М3). б) Является ли операция композиции машин коммутативной?
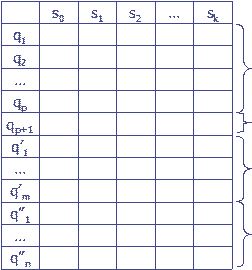
Окончательно машину из примера 9 мы можем записать: С°А°А°А или С°А3, если условиться считать Даны 3 машины М1, М2, М3, имеющие общий алфавит А = {s0, s1, s2,..., sk} и состояния q0, q1,..., qp; q'0, q'1,..., q'm; q''0, q''1,..., q''n соответственно. Ветвлением машин M1, M2, М3 называется машина, обозначаемая
Проиллюстрируем теперь программу машины из примера 10 (табл. 16).
Таблица 16
Программа машины из примера 10 запишется, как видно, следующим образом: Дальнейший анализ программы машины из примера 10 показывает, что машина M1— это машина l, машину М2 можно представить в виде композиции машин r и С (r°С), а М3— в виде r°С°А. Тогда машина из примера 10 окончательно запишется так:
Как видно, из простых (элементарных) машин Тьюринга l, r, С, А с помощью операций композиции и ветвления сконструировали более сложную машину Тьюринга (пример 10). Дана машина М, имеющая алфавит А={s0, s1, s2,..., sk} и состояния q0, q1, …, qp. Программа машины М содержит по крайней мере две команды с заключительным состоянием q0. Будем говорить, что машина М' получена из машины М с помощью операции зацикливания, если в одной из команд машины М, содержащих состояние q0, это состояние заменено на одно из состояний q1, q2, …, qp.
Так, машина из примера 11 получена с помощью операции зацикливания из машины с программой, данной в таблице 17. Таблица 17
Действительно, эта программа содержит две команды с заключительным состоянием q0: s0Лq0 и s0Нq0. Заменив в команде s0Нq0 состояние q0 состоянием q1 получили машину из примера 11.
Проанализируем теперь программу этой машины, данную в таблице 18.
Работа этой машины может быть следующим образом описана в терминах машин Р, Q, R. Сначала используется машина Р, затем в соответствии с тем, обозревает машина Р в состоянии q2 пустую ячейку или ячейку с буквой |, используется машина R или Q соответственно. В случае если используется машина Q, ее результат подается в Р. Записать это можно следующим образом:
|
имеющая алфавит А и состояния q0, q1, q2,..., qp, qp+1, q'1,..., q'm, q''1, q''2,..., q''n. Программа этой машины строится из программ машин M1, M2, M3 так, как показано в следующей таблице:
Таблица 18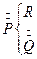
, где точки обозначают, что результат работы машины Q подается обратно в качестве входных данных для машины Р.
