Относительное положение плоскости и поверхности.
Относительное положение плоскостей Задание 1.2. Через прямую DЕ провести плоскость, перпендикулярную плоскости треугольника ABC. Построить линию пересечения двух плоскостей, заданных треугольниками, определить видимость. Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. Искомая плоскость должна содержать в себе заданную прямую Алгоритм решения задачи: 1. Строим плоскость, перпендикулярную плоскости треугольника 2. Две плоскости пересекаются по прямой линии. Для построения линии пересечения необходимо найти две точки, одновременно принадлежащие двум плоскостям. Точка 3. Определим видимость пересекающихся плоскостей. Видимость плоскостей определяется с помощью конкурирующих точек. Видимость стороны Относительное положение плоскости и поверхности.
|
и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость треугольника 
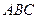. (Например, из точки 
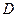- перпендикуляр 
).
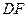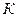принадлежит треугольнику 
. Вторую точку 
определяем, используя алгоритм нахождения точки пересечения прямой 
