1. В условии задачи заданы поверхности: два усеченных конуса.
2. Обе поверхности являются поверхностями вращения, оси вращения поверхностей пересекаются в точке  и лежат в одной плоскости. Эта плоскость параллельна фронтальной плоскости проекций и является плоскостью симметрии для заданных поверхностей. Следовательно, задачу можно решить способом концентрических вспомогательных сфер. Линия пересечения поверхностей вращения - пространственная кривая четвертого порядка.
и лежат в одной плоскости. Эта плоскость параллельна фронтальной плоскости проекций и является плоскостью симметрии для заданных поверхностей. Следовательно, задачу можно решить способом концентрических вспомогательных сфер. Линия пересечения поверхностей вращения - пространственная кривая четвертого порядка.
3. Точки пересечения очерков поверхностей  и
и 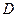 принадлежат линии пересечения поверхностей, т.к. располагаются в плоскости симметрии и являются характерными точками линии пересечения. Центром концентрических сфер является точка пересечения осей вращения поверхностей - точка
принадлежат линии пересечения поверхностей, т.к. располагаются в плоскости симметрии и являются характерными точками линии пересечения. Центром концентрических сфер является точка пересечения осей вращения поверхностей - точка  .
.
4. Для определения величины минимальной вспомогательной сферы, из точки пересечения осей вращения  проводим перпендикуляры на очерковые образующие пересекающихся поверхностей. Минимальная сфера должна быть вписана в большую поверхность. В рассматриваемой задаче большей поверхностью является усеченный конус. Радиус минимальной сферы обозначим
проводим перпендикуляры на очерковые образующие пересекающихся поверхностей. Минимальная сфера должна быть вписана в большую поверхность. В рассматриваемой задаче большей поверхностью является усеченный конус. Радиус минимальной сферы обозначим  . Радиус максимальной сферы
. Радиус максимальной сферы 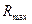 равен расстоянию от центра концентрических сфер
равен расстоянию от центра концентрических сфер  до наиболее удаленной точки пересечения очерков
до наиболее удаленной точки пересечения очерков 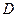
5. Вспомогательные промежуточные сферы проводим произвольным радиусом, но больше  и меньше
и меньше 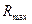 . Вспомогательная сфера пересекает каждую из заданных поверхностей по окружности, плоскость которой перпендикулярна оси вращения поверхности и проецируется на фронтальной плоскости проекций в прямую линию, перпендикулярную оси вращения поверхности. Проекции окружностей пересекаются в точках
. Вспомогательная сфера пересекает каждую из заданных поверхностей по окружности, плоскость которой перпендикулярна оси вращения поверхности и проецируется на фронтальной плоскости проекций в прямую линию, перпендикулярную оси вращения поверхности. Проекции окружностей пересекаются в точках 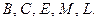 , принадлежащих обеим поверхностям. Это искомые точки, принадлежащие линии пересечения поверхностей.
, принадлежащих обеим поверхностям. Это искомые точки, принадлежащие линии пересечения поверхностей.
6. Построенные фронтальные проекции точек 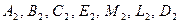 соединим плавной видимой кривой линией.
соединим плавной видимой кривой линией.
Задание 4. 2. Построить развертку поверхности 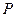 .
.
1. Для построения развертки поверхности, часть усеченного конуса ограниченную линией пересечения и верхним основанием начертим отдельно. Развертку прямого кругового конуса строим способом нормального сечения. Аппроксимируем поверхность усеченного конуса вписанной в него многогранной пирамидой. Для этого в круговое основание конуса впишем правильный двенадцатиугольник. Через вершины многоугольника проводим ребра пирамиды. Развертка прямого кругового конуса - часть кругового сектора, радиус которого равен величине очерковой образующей конуса  или
или 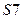 . Очерковые образующие
. Очерковые образующие  и
и 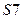 проецируются в натуральную величину на фронтальную плоскость проекций, так как являются фронтальными прямыми.
проецируются в натуральную величину на фронтальную плоскость проекций, так как являются фронтальными прямыми.
Длина дуги сектора равна периметру двенадцатиугольника, вписанного в круговое основание  .
.
2. Натуральную величину образующих конуса  определим способом вращения вокруг оси
определим способом вращения вокруг оси 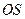 , перпендикулярной горизонтальной плоскости проекций.
, перпендикулярной горизонтальной плоскости проекций.
3. Построенные точки  соединим плавной кривой линией.
соединим плавной кривой линией.

 и лежат в одной плоскости. Эта плоскость параллельна фронтальной плоскости проекций и является плоскостью симметрии для заданных поверхностей. Следовательно, задачу можно решить способом концентрических вспомогательных сфер. Линия пересечения поверхностей вращения - пространственная кривая четвертого порядка.
и лежат в одной плоскости. Эта плоскость параллельна фронтальной плоскости проекций и является плоскостью симметрии для заданных поверхностей. Следовательно, задачу можно решить способом концентрических вспомогательных сфер. Линия пересечения поверхностей вращения - пространственная кривая четвертого порядка. и
и 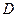 принадлежат линии пересечения поверхностей, т.к. располагаются в плоскости симметрии и являются характерными точками линии пересечения. Центром концентрических сфер является точка пересечения осей вращения поверхностей - точка
принадлежат линии пересечения поверхностей, т.к. располагаются в плоскости симметрии и являются характерными точками линии пересечения. Центром концентрических сфер является точка пересечения осей вращения поверхностей - точка  . Радиус максимальной сферы
. Радиус максимальной сферы 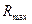 равен расстоянию от центра концентрических сфер
равен расстоянию от центра концентрических сфер 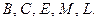 , принадлежащих обеим поверхностям. Это искомые точки, принадлежащие линии пересечения поверхностей.
, принадлежащих обеим поверхностям. Это искомые точки, принадлежащие линии пересечения поверхностей.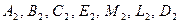 соединим плавной видимой кривой линией.
соединим плавной видимой кривой линией.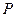 .
. или
или 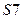 . Очерковые образующие
. Очерковые образующие  .
. определим способом вращения вокруг оси
определим способом вращения вокруг оси 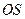 , перпендикулярной горизонтальной плоскости проекций.
, перпендикулярной горизонтальной плоскости проекций. соединим плавной кривой линией.
соединим плавной кривой линией.


