Задание 2.1. Построить проекции сечения комбинированной поверхности плоскостью α.Плоскость пересекает поверхность по линии, все точки которой одновременно принадлежат поверхности и плоскости. Эта линия называется линией сечения поверхности плоскостью. При построении проекций точек линии сечения используют способ вспомогательных секущих плоскостей: - проводят вспомогательные плоскости, которые пересекают поверхность по простым сечениям (окружность, прямоугольник, треугольник, угольник); строят несколько сечений; - искомые точки, принадлежащие поверхности и заданной плоскости Алгоритм решения задачи: 1. Заданная плоскость 2. Точки пересечения фронтального следа плоскости и очерков поверхностей определяют характерные точки сечения Сечение тора заданной плоскостью 3. Плоскость
|
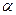, определяющие контур сечения, находятся на пересечении заданной плоскости 
) поверхности совпадает с фронтальным следом плоскости 
.
) принадлежит фронтальному следу плоскости. Горизонтальная проекция точек сечения совпадает с горизонтальной проекцией треугольника. Профильную проекцию треугольника строим в проекционной связи по горизонтальной и фронтальной проекциям.
