Задание 3. 1. Построить линии пересечения заданных поверхностей способом секущих плоскостей.
1. Заданная фигура состоит из усеченного конуса, не полного цилиндра и сферы. 2. Сфера - нелинейчатая поверхность вращения, образующей является окружность. Цилиндр - поверхность вращения с прямолинейной образующей. Ось вращения цилиндра перпендикулярна фронтальной плоскости проекций Усеченный конус - поверхность вращения с прямолинейной образующей, которая пересекает ось вращения в постоянной точке S. Ось вращения усеченного конуса перпендикулярна горизонтальной плоскости проекции 3. Линия пересечения усеченного конуса и сферы - пространственная кривая. Характерными точками линии пересечения усеченного конуса и сферы, является: точки пересечения очерков поверхностей самая ближняя Для построения линии пересечения сферы и цилиндра проводим вспомогательные горизонтальные секущие плоскости 4. Профильную проекцию линии пересечения усеченного конуса и сферы строим в проекционной связи по горизонтальной и профильной проекциям. 5. На фронтальной плоскости проекции линия пересечения видима, на горизонтальной плоскости проекции не видима, а на профильной плоскости проекции видима. 6. Линия пересечения усеченного конуса и цилиндра пространственная кривая. Характерными точками линии пересечения усеченного конуса и цилиндра являются точки пересечения очерков поверхностей на фронтальной плоскости проекции: точки 1, 2, 13. 7. Для построения промежуточных точек 3, 4, 5,6, 7,8, 9, 10, 11, 12, проводим вспомогательные горизонтальные секущие плоскости 8. На фронтальной и профильной плоскости проекций линия пересечения видима. На горизонтальной плоскости проекции линия видима на участке 5, 7, 9, 11, 13, 12, 10, 8, 6, а на участках 1, 3, 5 и 2, 4, 6 не видима.
|

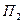 , все его образующие являются горизонтально проецирующими прямыми.
, все его образующие являются горизонтально проецирующими прямыми.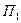 .
.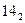 ;
;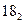 и самая удаленная
и самая удаленная 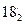 точки линии пересечения по отношению к наблюдателю.
точки линии пересечения по отношению к наблюдателю.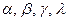 , которые пересекают сферу по окружности и усеченный конус по окружности. Радиусы окружностей - расстояние от оси вращения поверхности до очерка поверхности. Данные окружности проецируются в натуральную величину на горизонтальную плоскость проекции и пересекаются в точках 15, 16, 17, 18, принадлежащих линии пересечения сферы и усеченного конуса.
, которые пересекают сферу по окружности и усеченный конус по окружности. Радиусы окружностей - расстояние от оси вращения поверхности до очерка поверхности. Данные окружности проецируются в натуральную величину на горизонтальную плоскость проекции и пересекаются в точках 15, 16, 17, 18, принадлежащих линии пересечения сферы и усеченного конуса.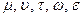 , которые пересекают цилиндр по прямоугольникам, а усеченный конус по окружностям. Радиусы окружностей - расстояние от оси вращения поверхности до очерка поверхности. Сечения (окружности) проецируются в натуральную величину на горизонтальную плоскость проекции. Точки пересечения прямоугольника и окружности искомые точки линии пересечения поверхностей. Для построения профильной проекций точек 1, 2, 3, 4, 5,6, 7,8, 9, 10, 11, 12, 13 проводим линии связи от горизонтальной проекции этих точек до профильных проекций секущих плоскостей
, которые пересекают цилиндр по прямоугольникам, а усеченный конус по окружностям. Радиусы окружностей - расстояние от оси вращения поверхности до очерка поверхности. Сечения (окружности) проецируются в натуральную величину на горизонтальную плоскость проекции. Точки пересечения прямоугольника и окружности искомые точки линии пересечения поверхностей. Для построения профильной проекций точек 1, 2, 3, 4, 5,6, 7,8, 9, 10, 11, 12, 13 проводим линии связи от горизонтальной проекции этих точек до профильных проекций секущих плоскостей 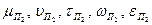 .
.


