Основные геодезические задачи
При переходе от измеряемых линейно-угловых величин к координатам точек местности решают следующие основные типы геодезических задач.
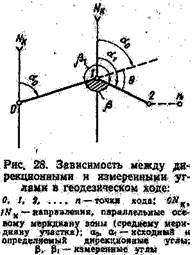
Вычисление дирекционных углов направлений. В геодезическом ходе, представляющем собой построение в виде ломаной линии с точками 0, 1, 2,..., η (рис. 28), легко установить связь между измеренными углами β и β1, исходным дирекционным углом предыдущего ао и определяемым дирекционным углом O1 последующего направлений, если принять во внимание, что α1 = αο+Θ, где Θ= 180°— β = β,—180°. Отсюда В этих формулах β — правый, βι — левый по ходу углы, если считать, что ход направлен в сторону возрастания номеров вершин. Чаще всего принято измерять правые углы хода.
1. Возможно непосредственное измерение базиса AC = b (рис. 29, а) и примыкающих к нему углов α и у. Тогда находят β= 180°—(α + γ) и по теореме синусов вычисляют a = bsina/sinp; c — b sin y /sin β. На практике принято для контроля измерять в треугольнике ABC и угол β, а также базис b' и углы α', β', γ' в треугольнике ABC, смежном с данным. В стесненных условиях лесной местности допускается определять недоступное расстояние AB из решения прямоугольного треугольника. При точке А (рис. 29, а) строят прямой угол, измеряют базис b и острые углы в точках B и C. 2. Возможно непосредственное измерение сторон а и b (см. рис. 29, б) и угла γ. Тогда, используя теоремы косинусов и синусов, находят
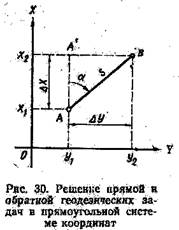
Прямая геодезическая задача. По данным координатам x1 и y1 точки А (рис. 30), дирекционному углу α направления с нее на точку В ирасстоянию S между ними требуется найти координаты x 2 и у2 точки В. Вычисляют длину катетов Ax и Ay прямоугольного треугольника AA'В, которые называют приращениями координат
Координаты точки находят по формулам Обратная геодезическаязадача. По данным координатам точек A(x1, у1) и В(х2, у2) требуется найти расстояние S и дирекционный угол направления с одной точки на другую (см. рис. 30). Вычисляют разности абсцисс иординат точек
а затем румб направления AB по формуле
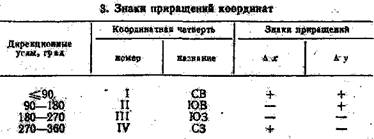
По знакам разностейординат и абсцисс, пользуясь табл. 3, определяют номер координатной четверти, чтобы перевести румб в дирекционный угол. Расстояние между точками вычисляют по формулам Методы определения планового положения точек местности
Координаты пунктов съемочного обоснования определяют построением геодезических сетей методами полигонометрии, триангуляции и трилатерации. Ход полигонометрии (рис. 31) опирается на исходные стороны AB и CD геодезической сети. В ходе
Трилатерация — метод определения координат пунктов в сети такой же формы, как и при триангуляции, но в ней измеряют все стороны и некоторые углы.
|

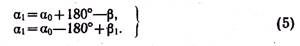
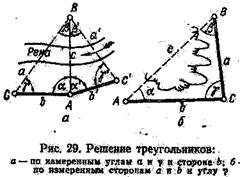 Решение треугольни ков.Для определения расстояний и углов, которые невозможно или нецелесообразно измерять непосредственно на местности, прибегают к построениям в виде треугольников. В них измеряют не менее трех линейных и угловых элементов, по которым вычисляют остальные. Рассмотрим следующие типичные случаи.
Решение треугольни ков.Для определения расстояний и углов, которые невозможно или нецелесообразно измерять непосредственно на местности, прибегают к построениям в виде треугольников. В них измеряют не менее трех линейных и угловых элементов, по которым вычисляют остальные. Рассмотрим следующие типичные случаи.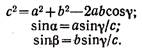
 Второй случай особенна характерен для лесной съемки, когда полученные при решении треугольника величины используют, чтобы указать направление прорубки просек (визиров) и определить их длину.
Второй случай особенна характерен для лесной съемки, когда полученные при решении треугольника величины используют, чтобы указать направление прорубки просек (визиров) и определить их длину.
 Приращения координат — проекции отрезка AB на оси координат. Они могут быть положительными или отрицательными в зависимости от величины дирекцион-ного угла α направления AB. Практически приращения координат вычисляют, пользуясь румбами направлений. Тогда изнаки приращений определяют по названиям румбов (табл. 3).
Приращения координат — проекции отрезка AB на оси координат. Они могут быть положительными или отрицательными в зависимости от величины дирекцион-ного угла α направления AB. Практически приращения координат вычисляют, пользуясь румбами направлений. Тогда изнаки приращений определяют по названиям румбов (табл. 3).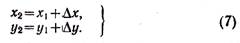
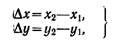

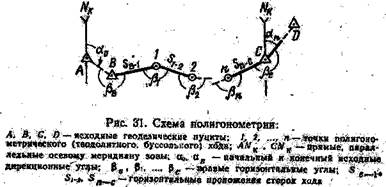 известны дирекционные углы α0 и αп, а также координаты начальной и конечной точек хода xь, уь и хс, ус· На местности измеряют углы βb, β1, β2,..., βn, βε и расстояния Sb-i, S1-2, S2-3,..., Sn-c Из вычислений по (5) получают дирекционные углы всех сторон хода, а затем по (6) и (7) — приращения координат и координаты точек 1, 2, 3,..., п. На лесных съемках применяют простейшие виды полигонометрии — теодолитные и буссольные ходы.
известны дирекционные углы α0 и αп, а также координаты начальной и конечной точек хода xь, уь и хс, ус· На местности измеряют углы βb, β1, β2,..., βn, βε и расстояния Sb-i, S1-2, S2-3,..., Sn-c Из вычислений по (5) получают дирекционные углы всех сторон хода, а затем по (6) и (7) — приращения координат и координаты точек 1, 2, 3,..., п. На лесных съемках применяют простейшие виды полигонометрии — теодолитные и буссольные ходы. Триангуляцию применяют для создания сети съемочного обоснования на открытых участках. Ее пункты размещают в виде цепочек треугольников и других систем (рис. 32), в которых измеряют все углы. Образованная треугольниками сеть обычно опирается на одну или две исходные стороны AB и CD. Если создают сеть в местной системе координат (рис. 32, б), то в ней измеряют не только углы, но также длину b и азимут A0 базисной стороны I — II. Сначала решают последовательно треугольники, начиная с того, который опирается на исходную (базисную) сторону, и находят длину всех сторон сети. Затем по начальному дирекционному углу (азимуту) и измеренным углам вычисляют дирекционные углы всех сторон. Наконец, решая прямые геодезические задачи, последовательно находят координаты пунктов I, II, III и др.
Триангуляцию применяют для создания сети съемочного обоснования на открытых участках. Ее пункты размещают в виде цепочек треугольников и других систем (рис. 32), в которых измеряют все углы. Образованная треугольниками сеть обычно опирается на одну или две исходные стороны AB и CD. Если создают сеть в местной системе координат (рис. 32, б), то в ней измеряют не только углы, но также длину b и азимут A0 базисной стороны I — II. Сначала решают последовательно треугольники, начиная с того, который опирается на исходную (базисную) сторону, и находят длину всех сторон сети. Затем по начальному дирекционному углу (азимуту) и измеренным углам вычисляют дирекционные углы всех сторон. Наконец, решая прямые геодезические задачи, последовательно находят координаты пунктов I, II, III и др.


