Задача 9. Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга
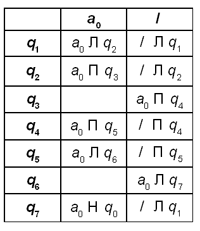
Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи. Идея решения (условие останова). На ленте есть два исходных массива штрихов.
Штрихи начинаем стирать с левого конца массива m. И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n. Но прежде чем стереть правый штрих в массиве n, проверяем, единственный он (т.е. последний, который надо стереть) или нет. Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу. Состояние q 1 — поиск разделителя между массивами штрихов при движении справа налево; состояние q 2 — поиск левого штриха в массиве m; состояние q 3 — удаление левого штриха в массиве m; состояние q 4 — поиск разделителя при движении слева направо; состояние q 5 — поиск правого штриха в массиве n; состояние q 6 — проверка единственности этого штриха в массиве n, т.е. определяем, был ли он последним; состояние q 7 — если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.
|