Свойства определителей
§ Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): § При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится. § Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. § Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю. § Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1). § Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. § Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
4) Алгебраическим дополнением элемента
где Название «алгебраическое дополнение» связано с формулами разложения определителя матрицы по строке (по столбцу):
Лемма о фальшивом разложении определителя утверждает, что
Из этих утверждений следует алгоритм нахождения обратной матрицы: § заменить каждый элемент исходной матрицы на его алгебраическое дополнение, § транспонировать полученную матрицу - в результате будет получена союзная матрица, § разделить каждый элемент союзной матрицы на определитель исходной матрицы.
5) Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
|
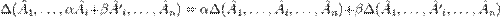, где 
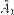и т. д. — строчки матрицы, 
— определитель такой матрицы.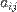
матрицы 
называется число
,
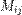— дополнительный минор, определитель матрицы, получающейся из исходной матрицы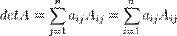 
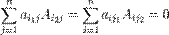при 
и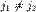 
.
