Формула Муавра и извлечение корней из комплексных чиселКорни пятой степени из единицы(вершины пятиугольника) Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид: zn = [ r (cos φ + i sin φ)] n = rn (cos n φ + i sin n φ), где r — модуль, а Аналогичная формула применима также и при вычислении корней n -ой степени из ненулевого комплексного числа: z 1 / n = [ r (cos(φ + 2π k) + i sin(φ + 2π k))]1 / n =
Отметим, что корни n -й степени из ненулевого комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n -угольника, вписанного в окружность радиуса
|
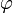— аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.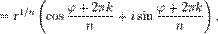
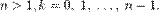
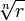с центром в начале координат (см. рисунок).
