Доказательство
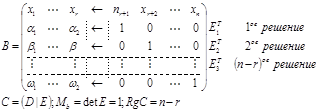 ….знак равенства (билет №8) (структура…) ….знак равенства (билет №8) (структура…)
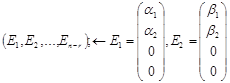 фср (х=) фср (х=)
Вопр№9 (Арифметическое пространство. Определение. Линейно независимые и линейно зависимые системы векторов и их свойства.)
Свойства линейных операций над векторами:

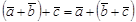

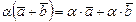 Линейная зависимость и независимость геометрических векторов:
Линейной комбинацией геометрических векторов
Линейная зависимость и независимость геометрических векторов:
Линейной комбинацией геометрических векторов 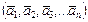 называется вектор называется вектор 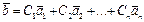 Системой из N векторов
Системой из N векторов  называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.
Если линейная комбинация всех этих векторов является нулевым вектором, то в случае равенства нулю всех «С»: называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.
Если линейная комбинация всех этих векторов является нулевым вектором, то в случае равенства нулю всех «С»:  , иначе если “Ci” не равно нулю, то система векторов называется линейно зависимой.
Теорема №1:
Два колиниарных вектора всегда линейно зависимы.
Теорема №2:
Три комплонарных вектора всегда линейно зависимы.
Теорема №3:
Любые четыре геометрических вектора линейно зависимы. , иначе если “Ci” не равно нулю, то система векторов называется линейно зависимой.
Теорема №1:
Два колиниарных вектора всегда линейно зависимы.
Теорема №2:
Три комплонарных вектора всегда линейно зависимы.
Теорема №3:
Любые четыре геометрических вектора линейно зависимы.

| Вопр№10 (. Базис и размерность арифметического пространства. Разложение вектора по базису.)
Базис:
Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов.
Базис на прямой является единственным вектором, параллельным данной прямой.
Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости.
Базис в пространстве – это любые три не комплонарных вектора.
Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса.
Теорема:
Для заданного вектора а и выбранного базиса разложение, по базису является единственным.
Координаты вектора в базисе:
Координатами любого вектора в пространстве (в базисе) называются коэффициенты его разложения базису.
| Вопр№11 (Собственные векторы и собственные числа матрицы. Определение, свойства. Характеристический многочлен. Нахождение собственных векторов и собственных чисел)
Арифметическим собственным вектором квадратной матрицы А порядка п называется такой не нулевой столбец: 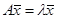 , где λ – собственной значение матрицы.
У каждой матрицы может быть пара из собственных векторов и собственных значений.
Множество всех собственных значений матрицы называется спектром. , где λ – собственной значение матрицы.
У каждой матрицы может быть пара из собственных векторов и собственных значений.
Множество всех собственных значений матрицы называется спектром.  – ненулевые решения однородной системы уравнений.
Однородная система имеет ненулевые решения, если ранг матрицы В равен количеству коэффициентов. – ненулевые решения однородной системы уравнений.
Однородная система имеет ненулевые решения, если ранг матрицы В равен количеству коэффициентов.
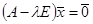 – характеристическое уравнение матрицы А. – характеристическое уравнение матрицы А.
 Проверить!!!¿¿¿
Рациональное алгебраическое уравнение степени N. Всегда имеет N корней, среди которых могут быть и кратные. Проверить!!!¿¿¿
Если определитель матрицы А равен нулю, то характеристический многочлен не содержит свободных членов.
У вырожденной матрицы хотя бы одно значение равно нулю. ¿¿¿…???
При этом сами фундаментальные решения образуют систему линейно независимых уравнений.
Свойства собственных векторов и собственных значений матрицы:
Максимальное количество линейно независимых собственных векторов, соответствующих данному собственному значению Проверить!!!¿¿¿
Рациональное алгебраическое уравнение степени N. Всегда имеет N корней, среди которых могут быть и кратные. Проверить!!!¿¿¿
Если определитель матрицы А равен нулю, то характеристический многочлен не содержит свободных членов.
У вырожденной матрицы хотя бы одно значение равно нулю. ¿¿¿…???
При этом сами фундаментальные решения образуют систему линейно независимых уравнений.
Свойства собственных векторов и собственных значений матрицы:
Максимальное количество линейно независимых собственных векторов, соответствующих данному собственному значению 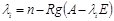 .
Линейная комбинация из собственных векторов соответствует одному и тому же, в свою очередь являющемуся собственным вектором для этого собственного значения.
Собственные векторы с попарно различными «чего-то такое???» значениями являются??? Проверить¿¿¿
Если матрица АТ=А, то все её собственные значения являются действительными числами.
Спектр вырожденной матрицы А содержит хотя бы один нулевой элемент.
Если матрица имеет пары комплексные сопряженные, То соответствующие им собственные векторы тоже комплексные
Для вычисления собственных значений матрицы необходимо составить характеристическое уравнение: .
Линейная комбинация из собственных векторов соответствует одному и тому же, в свою очередь являющемуся собственным вектором для этого собственного значения.
Собственные векторы с попарно различными «чего-то такое???» значениями являются??? Проверить¿¿¿
Если матрица АТ=А, то все её собственные значения являются действительными числами.
Спектр вырожденной матрицы А содержит хотя бы один нулевой элемент.
Если матрица имеет пары комплексные сопряженные, То соответствующие им собственные векторы тоже комплексные
Для вычисления собственных значений матрицы необходимо составить характеристическое уравнение: 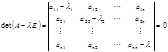 составив уравнение можно найти его корни, они-то и будут собственными значениями матрицы.
Собственные векторы матрицы соответствуют собственным значениям матрицы. составив уравнение можно найти его корни, они-то и будут собственными значениями матрицы.
Собственные векторы матрицы соответствуют собственным значениям матрицы.
| Вопр№12 (. Базис на прямой, на плоскости и в пространстве. Координаты вектора в данном базисе. Линейные операции над векторами в координатной форме)
Базис:
Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов. Базис на прямой является единственным вектором, параллельным данной прямой. Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости.
Базис в пространстве – это любые три не комплонарных вектора. Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса.
Теорема: Для заданного вектора а и выбранного базиса разложение, по базису является единственным.
Координаты вектора в базисе:
Координатами любого вектора в пространстве (в базисе) называются коэффициенты его разложения базису.
Свойства линейных операций над векторами:

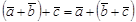

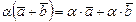
|
Вопр№13.(Скалярное произведение векторов. Свойства. Выражение через координаты сомножителей) Проекция вектора на вектор:
 Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
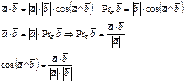 Свойства:
Свойства:
 – Коммутативность. – Коммутативность.



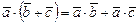
 Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.
Применение скалярного произведения:
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.
Применение скалярного произведения:
 Определение перпендикулярности векторов, как скалярное произведение, равное нулю.
Определение перпендикулярности векторов, как скалярное произведение, равное нулю.
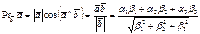

| Вопр№14 (Ориентация тройки векторов. Векторное произведение векторов. Свойства. Выражение через координаты сомножителей) Векторное произведение векторов.
Свойства.Геометрический смысл. Выражение через координаты сомножителей.
Векторным произведением векторов называется вектор, обозначаемый 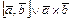 , который обладает двумя свойствами:
Перпендикулярен двум исходным векторам.
Составляет с исходными векторами правую тройку[1] , который обладает двумя свойствами:
Перпендикулярен двум исходным векторам.
Составляет с исходными векторами правую тройку[1]
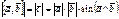 Направление результирующего вектора определяется по правилу буравчика.
Свойства векторного произведения:
Направление результирующего вектора определяется по правилу буравчика.
Свойства векторного произведения:
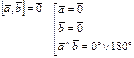 – проверка на колиниарности. – проверка на колиниарности.


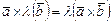

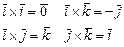
| Вопр№15 (Смешанное произведение векторов. Геометрический смысл. Свойства. Выражение через координаты сомножителей)
Смешанным произведением трёх векторов называется число, обозначаемое  , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых. , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.

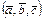 >0, когда >0, когда 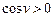 , а значит угол v – острый, следовательно, вектора составляют правую тройку. , а значит угол v – острый, следовательно, вектора составляют правую тройку.
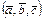 <0, когда <0, когда 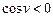 , а значит угол v – тупой, следовательно, вектора составляют левую тройку.
Свойства смешанного произведения: , а значит угол v – тупой, следовательно, вектора составляют левую тройку.
Свойства смешанного произведения:
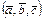 =0 тогда, когда =0 тогда, когда 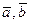 комплонарны. комплонарны.
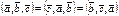

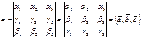
| Вопр№16 (16. Понятие об уравнении линии и поверхности. Алгебраические линии и поверхности, их порядок. Уравнение окружности и сферы)
| 
Первых… 
тройку 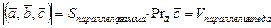

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Медицинская документация родильного дома Учетные формы родильного дома № 111/у Индивидуальная карта беременной и родильницы
№ 113/у Обменная карта родильного дома...
Основные разделы работы участкового врача-педиатра Ведущей фигурой в организации внебольничной помощи детям является участковый врач-педиатр детской городской поликлиники...
Ученые, внесшие большой вклад в развитие науки биологии Краткая история развития биологии. Чарльз Дарвин (1809 -1882)- основной труд « О происхождении видов путем естественного отбора или Сохранение благоприятствующих пород в борьбе за жизнь»...
|
Правила наложения мягкой бинтовой повязки 1. Во время наложения повязки больному (раненому) следует придать удобное положение: он должен удобно сидеть или лежать...
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
САНИТАРНО-МИКРОБИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ ВОДЫ, ВОЗДУХА И ПОЧВЫ Цель занятия.Ознакомить студентов с основными методами и показателями...
|
|