Вопр№17 (Прямая линия на плоскости (общее, векторное, векторно-параметрическое, каноническое, с угловым коэффициентом уравнение прямой). Расстояние от точки до прямой) На плоскости задана прямоугольная декартова система координат.
Уравнение  называется уравнением линии L на плоскости, если координаты всех точек линии подчиняются закону F, а координаты всех точек, не лежащих на линии  .Линия – это геометрическое место точек, координаты которых удовлетворяют закону 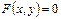 – основное уравнение прямой на плоскости. Векторное уравнение прямой на плоскости:
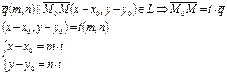Параметрическое уравнение прямой на плоскости:
Каноническое уравнение прямой на плоскости:
Расстояние от точки до прямой:
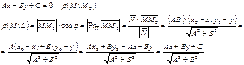Угол между прямыми:
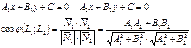
| Вопр№18 (. Условие параллельности и перпендикулярности, угол между прямыми на плоскости)
| Вопр№19 (Плоскость как поверхность 1-го порядка. Различные виды уравнений плоскости. Условие параллельности и перпендикулярности, угол между плоскостями. Расстояние от точки до плоскости)
| Вопр№20 (. Прямая линия в пространстве. Каноническое и общее уравнения прямой в пространстве)
|
| Вопр№21 (Условие параллельности и перпендикулярности двух прямых. Угол между прямыми (в пространстве). Взаимное расположение прямой и плоскости)
| Вопр№22 (. Кривые 2-го порядка. Канонические уравнения эллипса, гиперболы, параболы)
| Вор№23 (Поверхности 2-го порядка. Уравнения эллипсоида, гиперболоида, конуса)
|
|
[1] Тройка векторов называется правой, если из третьего вектора кротчайший поворот от первого ко второму виден, как поворот против часовой стрелки.
