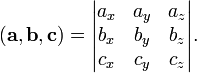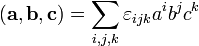Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы
Прямые, на которых расположены векторы Таким образом, под суммой векторов 7) Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов. Если векторы
Главная особеннность декартовых базисов состоит в том, что координаты любого вектора в этом базисе равны проекциям этого вектора на три взаимно ортогональных направления, определяемых ортами. Эти направления называют координатными осями декартовой системы координат (рис. 9): оси
Рис.9 Декартова система координат
где проекции вектора
Если орты декартовой системы координат связаны между собой следующими соотношениями
то такая система координат называется правой. В заданной декартовой системе координат для каждой точки пространства можно ввести так называемый радиус-вектор
Рис.10. К определению радиус-вектора
Модуль радиус-вектора
Тогда, декартов базис - это тройка векторов
Координаты вектора
и т. д. В дальнейшем будет рассматриваться только трехмерное пространство, поэтому, если специально не указано, то индексы будут принимать значения 1, 2, 3. Например,
В новых обозначениях разложение вектора
а радиус-вектора
В этих выражениях индексы
При использовании этого правила следует следить, чтобы количество свободных индексов в правой и левой частях выражения было одинаковым и не менялось при выполнении каких-либо преобразований. Например, из (1) следует, что 8) Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Обычно используется одно из следующих обозначений:
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
Обычно предполагается что скалярное произведение положительно определено, то есть
Если этого не предполагать, то произведение называется индефинитным. Скалярным произведением в векторном пространстве 1. для любых трех элементов 2. для любых 3. для любого Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
9) Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции«векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно являетсяантикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны. Векторное произведение определено только в трёхмерном и семимерном пространстве. Результат векторного произведения, как и скалярного, зависит от метрикиЕвклидова пространства. В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности». Векторным произведением вектора § длина вектора
§ вектор § вектор § в случае пространства Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левойпрямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов. Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное. 10) Сме́шанное произведе́ние
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр). Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами § Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
§ Смешанное произведение
§ Смешанное произведение
В частности, § Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю. § Геометрический смысл — Смешанное произведение
Три вектора, определяющие параллелепипед. § Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов). 11)
|

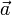 и
и 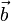 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы  и
и 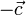 , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы 
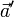 и
и 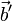 , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы  образуют пару (векторов).
образуют пару (векторов).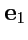 ,
, 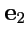 ,
, 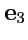 взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как
взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как 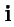 ,
, 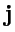 ,
, 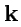 . Согласно определению
. Согласно определению
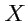 ,
, 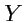 и
и 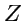 . Точка пересечения координатных осей 0 называется началом координат. Тогда
. Точка пересечения координатных осей 0 называется началом координат. Тогда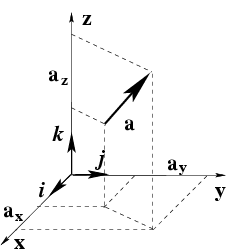
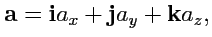
 определены как
определены как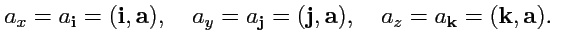

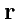 - направленный отрезок, начинающийся в начале координат и заканчивающийся в данной точке. Координаты радиус-вектора совпадают с декартовыми координатами соответствующей точки (рис. 10):
- направленный отрезок, начинающийся в начале координат и заканчивающийся в данной точке. Координаты радиус-вектора совпадают с декартовыми координатами соответствующей точки (рис. 10):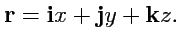

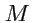 -
-  "привязан" к системе координат и зависит от выбора начала координат. Отметим также, что три орта
"привязан" к системе координат и зависит от выбора начала координат. Отметим также, что три орта 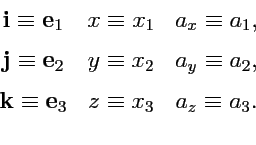

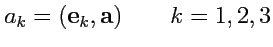
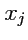 - это какая-то из трех координат радиус-вектора
- это какая-то из трех координат радиус-вектора  запишется как
запишется как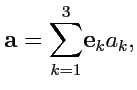
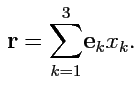
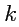 уже не свободны, это индексы суммирования и от них правая часть не зависит (их можно обозначить как угодно), что видно по левой части, где находится вектор. Это соответствие будет выполняться всегда и поэтому нет необходимости писать знак суммы
уже не свободны, это индексы суммирования и от них правая часть не зависит (их можно обозначить как угодно), что видно по левой части, где находится вектор. Это соответствие будет выполняться всегда и поэтому нет необходимости писать знак суммы 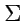 , а для таких выражений принято правило суммирования Эйнштейна: если выражение с индексами содержит парные индексы, то по ним предполагается суммирование (в 3-х мерном пространстве значения индексов изменяются от 1 до 3). Тогда, разложения вектора
, а для таких выражений принято правило суммирования Эйнштейна: если выражение с индексами содержит парные индексы, то по ним предполагается суммирование (в 3-х мерном пространстве значения индексов изменяются от 1 до 3). Тогда, разложения вектора 
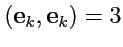 . Иногда индекс суммирования может быть свернут арифметическим действием. Так,
. Иногда индекс суммирования может быть свернут арифметическим действием. Так,  следует понимать как
следует понимать как 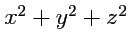 , так как
, так как 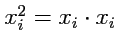 .
.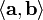 ,
, ,
, ,
, .
. для всех
для всех 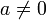 .
. над полем
над полем  называется функция
называется функция  для элементов
для элементов 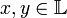 , принимающая значения в
, принимающая значения в 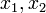 и
и 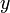 пространства
пространства  справедливо равенство
справедливо равенство  (линейность скалярного произведения по первому аргументу);
(линейность скалярного произведения по первому аргументу); и
и 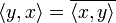 , где черта означает комплексное сопряжение (эрмитова симметричность);
, где черта означает комплексное сопряжение (эрмитова симметричность);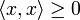 , причем
, причем  только при
только при 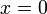 (положительная определенность скалярного произведения).
(положительная определенность скалярного произведения). действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.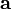 на вектор
на вектор 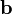 в пространстве
в пространстве 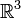 называется вектор
называется вектор  , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям: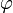 ; между ними
; между ними
 является правой.
является правой. требуется ассоциативность тройки векторов
требуется ассоциативность тройки векторов  .
.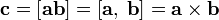
 векторов
векторов 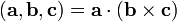 .
.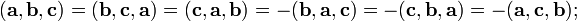

 и
и