Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости: ξ x + η y = 1. Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами. Уравнения прямой в пространстве Векторное параметрическое уравнение прямой в пространстве:
где Параметрическое уравнение прямой в пространстве:
где Каноническое уравнение прямой в пространстве:
где Общее векторное уравнение прямой в пространстве: Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
то уравнение прямой можно задать системой этих уравнений:
Взаимное расположение точек и прямых на плоскости Три точки
Отклонение точки
где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону. В пространстве расстояние от точки
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент t этой точки может быть найден по формуле
Взаимное расположение нескольких прямых на плоскости Две прямые, заданные уравнениями
или
пересекаются в точке
Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрами A 1, B 1, C 1, k 1 и b 1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой. Эти прямые параллельны, если A 1 B 2 − A 2 B 1 = 0 или k 1 = k 2, и перпендикулярны, если A 1 A 2 + B 1 B 2 = 0 или Любую прямую, параллельную A 1 x + B 1 y + C 1 = 0, можно выразить уравнением A 1 x + B 1 y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C 1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой. Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если
13) Изучение геометрических объектов с помощью метода координат начнем с простейших поверхностей и линий, а именно: плоскостей и прямых. Определение. Линейным уравнением относительно переменных x, y, z называется уравнение вида Ax + By + Cz + D = 0, где хотя бы один из коэффициентов А, В, С отличен от нуля. Теорема. Всякая плоскость в пространстве определяется линейным уравнением
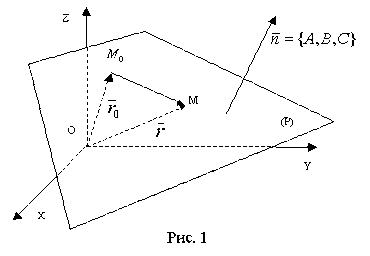
и обратно, всякое линейное уравнение (3) определяет плоскость в пространстве. Действительно, пусть в пространстве R3 задана плоскость (Р) (рис. 1).
Выбираем на ней какую-либо точку M0(x0, y0, z0), и в некоторой точке плоскости (P) построим ненулевой вектор
Уравнение (4) называется векторным уравнением плоскости. Т.к.
Уравнение (5) перепишем в виде:
где D = -Ax0 - By0 - Cz0, то есть получим уравнение (3). Это показывает, что любая плоскость может быть описана уравнением (3). Уравнение (3) называют общим уравнением плоскости, а уравнение (5) - уравнением плоскости, проходящей через заданную точку M0(x0, y0, z0). <p< p="">class="maintext">Отметим, что вектор Легко доказывается и обратное: дано уравнение Ax + By + Cz + D = 0 и нужно убедиться, что оно описывает плоскость в пространстве R3. Пусть (x0, y0, z0) - какое-либо решение данного уравнения. Тогда Ax0 + By0 + Cz0 + D = 0. Отсюда получаем D = -Ax0 - By0 - Cz0 и, подставляя в исходное уравнение, получаем: Следовательно, и равносильное ему уравнение Ax + By + Cz + D = 0 определяет плоскость. Теорема доказана. Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), принадлежащие плоскости и не лежащие на одной прямой. Возьмем текущую точку M(x, y, z) плоскости и организуем три вектора
Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть
Уравнение (6) и есть уравнение плоскости, проходящей через три заданные точки M1, M2, M3. При решении задач часто используется так называемое уравнение плоскости в отрезках на осях. Пусть в общем уравнении плоскости (3) A ≠ 0, B≠ 0, C≠ 0, D≠ 0. Перенесем свободный член D в правую часть и разделим обе части уравнения на - D, тогда получим:
где Уравнение (7) и называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz. Действительно, точка пересечения плоскости с осью, скажем, Ох имеет ординату у = 0 и аппликату z = 0. Но координаты этой точки (х,0,0) должны удовлетворять уравнению плоскости, т.е.
Отсюда получаем Полезно самостоятельно провести исследования общего уравнения плоскости (3), т.е. установить специфику пространственного расположения плоскости в случаях:
Решим теперь задачу о вычислении угла между двумя плоскостями. Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей. Если плоскости заданы своими общими уравнениями
то их нормальные векторы имеют вид
Условием параллельности двух плоскостей является условие
а условием перпендикулярности двух плоскостей является условие
14) Всякое уравнение первой степени относительно координат x, y, z Ax + By + Cz +D = 0 (3.1) задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости. Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0. Особые случаи уравнения (3.1): 1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат. 2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz. 3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz. 4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz. Уравнения координатных плоскостей: x = 0, y = 0, z = 0. Прямая в пространстве может быть задана: 1) как линия пересечения двух плоскостей,т.е. системой уравнений: A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (3.2) 2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями: = 3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
|


 — радиус-вектор некоторой фиксированной точки M 0, лежащей на прямой,
— радиус-вектор некоторой фиксированной точки M 0, лежащей на прямой, 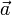 — ненулевой вектор, коллинеарный этой прямой,
— ненулевой вектор, коллинеарный этой прямой,  — радиус-вектор произвольной точки прямой.
— радиус-вектор произвольной точки прямой.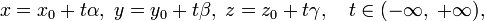
 — координаты некоторой фиксированной точки M 0, лежащей на прямой;
— координаты некоторой фиксированной точки M 0, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.
— координаты вектора, коллинеарного этой прямой.
 и
и 

 ,
,  и
и  лежат на одной прямой тогда и только тогда, когда выполняется условие
лежат на одной прямой тогда и только тогда, когда выполняется условие

 до прямой, заданной параметрическим уравнением
до прямой, заданной параметрическим уравнением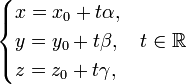





 .
.


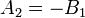 и
и  , то прямые
, то прямые 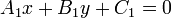 и
и  перпендикулярны.
перпендикулярны.
 , перпендикулярный плоскости (P). Для того, чтобы произвольная точка M(x, y, z) пространства принадлежала плоскости (P), необходимо и достаточно, чтобы
, перпендикулярный плоскости (P). Для того, чтобы произвольная точка M(x, y, z) пространства принадлежала плоскости (P), необходимо и достаточно, чтобы 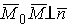 , то есть
, то есть
 и
и  , то скалярное произведение в (4) можем заменить через координаты сомножителей, а именно:
, то скалярное произведение в (4) можем заменить через координаты сомножителей, а именно: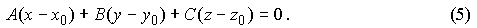


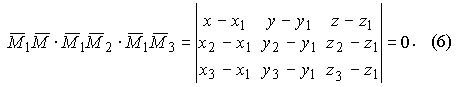


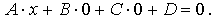
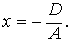


 и потому угол Θ; между плоскостями находим по формуле
и потому угол Θ; между плоскостями находим по формуле
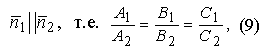

 ; (3.3)
; (3.3) . (3.4)
. (3.4)


