Необходимое и достаточное условие параллельности прямой и плоскости
В координатах:
где
В координатах:
16) Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F 1 и F 2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть | F 1 M | + | F 2 M | = 2 a, причем | F 1 F 2 | < 2 a.
§ Оптические § Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе. § Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся. § Если F 1 и F 2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F 1 X) равен углу между этой касательной и прямой (F 2 X). § Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы. § Эволютой эллипса является астроида. § Точки пересечения эллипса с осями являются его вершинами. § Эксцентриситет эллипса равен отношению § Эллипс также можно описать как § фигуру, которую можно получить из окружности, применяя аффинное преобразование § ортогональную проекцию окружности на плоскость. § Пересечение плоскости и кругового цилиндра
|
или 
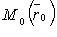перпендикулярно к плоскости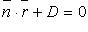 
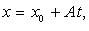
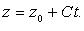
. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
