Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Длина дуги эллипса Длина дуги плоской линии определяется по формуле:
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:
После замены
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода
где Приближённые формулы для периметра
Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная. Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:
Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная. Cущественно лучшую точность при 0,05 < a / b < 20 обеспечивает формула Рамануджана:
При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная. Площадь эллипса и его сегмента Площадь эллипса вычисляется по формуле
Площадь сегмента между дугой, выпуклой влево, и хордой, проходящей через точки
Если эллипс задан уравнением Ax 2 + Bxy + Cy 2 = 1, то площадь можно определить по формуле
17) Гипе́рбола (др.-греч. ὑπερβολή, от др.-греч. βαλειν — «бросать», ὑπερ — «сверх») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F 1 и F 2 (называемых фокусами) постоянно. Точнее,
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
|




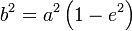 выражение для длины дуги принимает окончательный вид:
выражение для длины дуги принимает окончательный вид: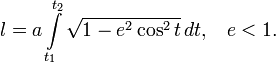
 . В частности, периметр эллипса равен:
. В частности, периметр эллипса равен: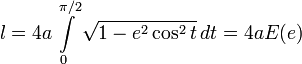 ,
, — полный эллиптический интеграл второго рода.
— полный эллиптический интеграл второго рода.
 , где
, где 


 и
и 

 .
. причем | F 1 F 2 | > 2 a > 0.
причем | F 1 F 2 | > 2 a > 0.


