Диаметры и центр кривой второго порядка
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:
Если выполняется условие Координаты центра
Решая эту систему относительно x 0 и y 0, получим:
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
где
|
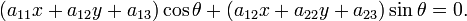
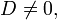то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают.
определяются системой уравнений: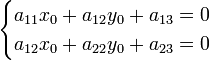
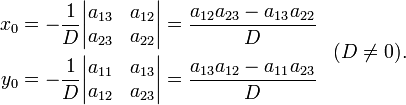
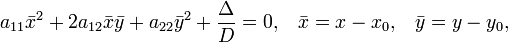
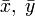— координаты относительно новой системы.
