Канонический вид
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты
Для центральной кривой в каноническом виде её центр 19) Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и даннойточки (называемой фокусом параболы). Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичнымэксцентриситетом. аноническое уравнение параболы в прямоугольной системе координат:
Квадратное уравнение
Уравнение Расчёт коэффициентов квадратного уравнения Если для уравнения
Свойства § Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе. § Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. § Для параболы Для параболы § Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе. § Парабола является антиподерой прямой. § Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб. § При вращении пар
|
и корни характеристического уравнения 
(см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
)
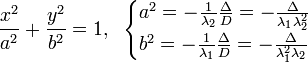
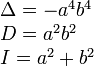
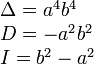
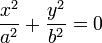
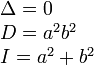
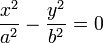
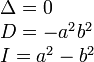
находится в начале координат.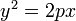
(или 
, если поменять местами оси).
при 
также представляет собой параболу и графически изображается той же параболой, что и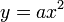 
, но в отличие от последней имеет вершину не в начале координат, а в некоторой точке 
, координаты которой вычисляются по формулам: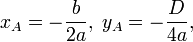
где D = b 2 − 4 ac - дискриминант
, а в случае переноса начала координат в точку 
, 
, 
, то его коэффициенты могут быть найдены так: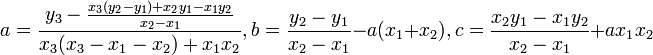
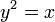фокус находится в точке (0,25; 0).
фокус находится в точке (0; f).
