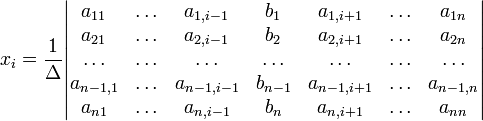Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Решения матричных уравнений Матричные уравнения могут иметь вид: АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица. Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы. Например, чтобы найти матрицу Тогда: Следовательно, чтобы найти решение 3) Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы — Размерность образа dim (im (A)) линейного оператора, которому соответствует матрица. Обычно ранг матрицы A обозначается 4) Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод. Для системы n линейных уравнений с n неизвестными (над произвольным полем)
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b 1, b 2,..., bn и x 1, x 2,..., xn, либо набор c 1, c 2,..., cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модулянад этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы. 5)Ме́тод Га́усса [1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные
|

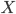 из уравнения
из уравнения 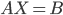 , необходимо умножить это уравнение на
, необходимо умножить это уравнение на 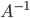 слева.
слева.
 , стоящие в правой части уравнения.
, стоящие в правой части уравнения.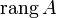 (
( ) или
) или 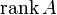 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английскогоязыка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английскогоязыка, в то время как первый — для немецкого, французского и ряда других языков.