Преобразование координат при замене базиса.
Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n -мерного линейного пространства Ln. Обозначим xe = (x 1, x 2,..., xn) и xf = (x' 1, x' 2,..., x'n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe = Ce→f·xf:
Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., e n: f1 = с 11· e2 + с 21 · e1 +... + сn 1 · e n, f2 = с 12· e1 + с 22 · e2 +... + сn 2 · e n, ..., f n = с 1 n · e2 +... + сnn · e n. Формулу преобразования координат вектора при изменении базиса принято записывать в виде xf = (Ce→f)− 1·xe ИЛИ Пусть в
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта матрица называется матрицей перехода от старого базиса к новому.
|
-мерном линейном пространстве 
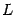выбран базис 
, который мы будем для удобства называть "старый" и другой базис 
, который мы будем называть "новый". Возьмем призвольный вектор 
из 
, а в новом --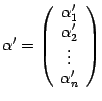 
. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
