Пусть V – линейное пространство, А – линейный оператор из  ,
,  и
и 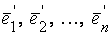 – два базиса в V и
– два базиса в V и  – формулы перехода от базиса
– формулы перехода от базиса  к базису
к базису  . Обозначим через
. Обозначим через 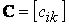 матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть
матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть  и
и  – матрицы оператора А в указанных базисах.
– матрицы оператора А в указанных базисах.
Теорема 7.1. Матрицы А и  оператора А в базисах
оператора А в базисах  и
и  связаны соотношением
связаны соотношением  .
.
Доказательство. При воздействии линейного оператора А вектор  пространства
пространства  переводится в вектор
переводится в вектор  этого пространства, т.е. справедливо равенство
этого пространства, т.е. справедливо равенство
 = А
= А  (7.3)
(7.3)
(в старом базисе) и равенство
 = А
= А 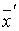 (7.4)
(7.4)
(в новом базисе). Так как 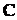 – матрица перехода от старого базиса к новому, то
– матрица перехода от старого базиса к новому, то
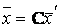 (7.5)
(7.5)
 (7.6)
(7.6)
Умножим равенство (7.5) слева на матрицу  , получим А
, получим А  = АC
= АC 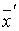 и с учетом (7.3)
и с учетом (7.3)  = АC
= АC 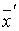 . Заменив левую часть полученного выражения в соответствии с (7.6), получим: С
. Заменив левую часть полученного выражения в соответствии с (7.6), получим: С  = АC
= АC 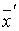 или
или  = С –1 АC
= С –1 АC 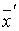 . Сравнивая найденное выражение с равенством (7.4), получим доказываемую формулу.
. Сравнивая найденное выражение с равенством (7.4), получим доказываемую формулу.
Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса
……………………..
Как уже отмечалось, в пространстве Rn существует множество различных базисов.
Пусть  и
и 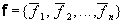 — двабазиса в Rn.
— двабазиса в Rn.
Обозначим  и
и  координаты векторов
координаты векторов 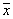 и
и  из Rn и матрицу оператора A соответственно в базисах
из Rn и матрицу оператора A соответственно в базисах  и
и 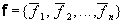 , а
, а  — матрица перехода от базиса
— матрица перехода от базиса  к базису
к базису 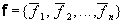 , т.е.
, т.е.
 ,
,
 ,
,

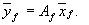
Тогда

откуда имеем
 — формулы преобразования матрицы линейного оператора при изменении базиса.
— формулы преобразования матрицы линейного оператора при изменении базиса.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = { a i j } = { A (e j) i }:

Координаты образа y = A (x) и прообраза x связаны соотношеннием:
y = A · x,



 ,
,  и
и 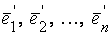 – два базиса в V и
– два базиса в V и  – формулы перехода от базиса
– формулы перехода от базиса  к базису
к базису  . Обозначим через
. Обозначим через 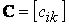 матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть
матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть  и
и  – матрицы оператора А в указанных базисах.
– матрицы оператора А в указанных базисах. оператора А в базисах
оператора А в базисах  .
. пространства
пространства  переводится в вектор
переводится в вектор  этого пространства, т.е. справедливо равенство
этого пространства, т.е. справедливо равенство = А
= А 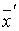 (7.4)
(7.4)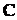 – матрица перехода от старого базиса к новому, то
– матрица перехода от старого базиса к новому, то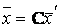 (7.5)
(7.5) (7.6)
(7.6) , получим А
, получим А  и
и 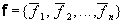 — двабазиса в Rn.
— двабазиса в Rn. и
и  координаты векторов
координаты векторов 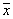 и
и  из Rn и матрицу оператора A соответственно в базисах
из Rn и матрицу оператора A соответственно в базисах  — матрица перехода от базиса
— матрица перехода от базиса  ,
, ,
,
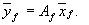

 — формулы преобразования матрицы линейного оператора при изменении базиса.
— формулы преобразования матрицы линейного оператора при изменении базиса.





