Задачи и их решенияЗадача 1. Над центром круглого стола диаметром 1,5 м на высоте 1 м подвешен точечный источник силой света 200 кд. Определите световой поток, падающий на горизонтальную поверхность стола, и среднюю освещенность этой поверхности.
Дано: d= 1,5 м, H = 1 м, I = 200 кд. __________ Ф–? E –? Решение Световой поток, падающий на поверхность стола, определяется по формуле
где h – высота сегмента, равная длине отрезка BC. Известно, что телесный угол при вершине конуса равен отношению площади сегментной поверхности к квадрату радиуса сферы:
Радиус сферы определяем из прямоугольного треугольника OCD:
Из рисунка видно, что высота сегмента h = R – H = 0,25 м. Подставляя найденные значения R и h в формулу
получаем:
Тогда величина светового потока, падающего на поверхность стола, равна:
Освещенность поверхности стола определяется по формуле
Задача 2. Над серединой стола на высоте 1,2 м висит точечный источник, сила света которого 100 кд. Определите наибольшую и наименьшую освещенность поверхности стола, если его длина 2 м, а ширина 1 м.
Решение Освещенность, создаваемая точечным источником света, равна
Из этой формулы видно, что освещенность максимальна в наиболее близкой к источнику точке стола и минимальна – в наиболее удаленной точке. На рис. 3 такими точками являются соответственно точка O и угловая точка стола, например точка C. По условию задачи SO = H, угол
Для определения освещенности в точке C находим расстояние от источника до этой точки и угол падения лучей:
Подставляя числовые значения в формулы для нахождения максимальной и минимальной освещенностей, получаем:
Задача 3. Точечный источник света S освещает горизонтальную поверхность (рис. 4). Определите, как изменится освещенность в точке A, в которую лучи падают перпендикулярно к поверхности, если сбоку от источника, на таком же расстоянии, поместить плоское зеркало, отражающее свет в эту точку. Коэффициент отражения зеркала считайте равным единице.
Дано: SA = SB = R, k = 1. Е/Е0–? Решение: При отсутствии плоского зеркала освещенность в точке A определяется по формуле:
Если сбоку поместить плоское зеркало, то освещенность в точке A будет равна сумме освещенностей, создаваемых двумя источниками: реальным источником S и мнимым S1, имеющими одинаковую силу света. Следовательно,
Из построения следует, что треугольник SBS1 равнобедренный, следовательно, SB = S1B = R. Расстояние от мнимого источника света S1 до точки A
Задача 4. При фотографировании объекта, помещенного на расстоянии 1 м от электрической лампочки силой света 40 кд, требовалось экспонирование в течение 2 с. Определите продолжительность экспонирования при использовании лампочки силой света 30 кд на расстоянии 1,5 м от объекта. Предполагается, что световая энергия, полученная объектом в обоих случаях, одинакова. Дано: I1 = 40 кд, R1 = 1 м, t1 = 2 с, I2 = 30 кд, R2 = 1,5 м, W1 = W2. _________ t2 –? Решение: Освещенность объекта равна:
Так как W1=W2, то
Задача 5. Точечный источник света, находящийся в вершине телесного угла 0,50 ср, излучает в него световой поток 50 лм. Определите силу света источника. I = dФv/dW I= Ф/ W = 50/0,5=100 кд
Задача 6. Определите телесный угол, внутри которого проходит световой поток 4 лм от точечного источника силой света 50 кд. Из формулы для силы света I = dФv/dW телесный угол W равен W = Ф/I = 4 лм / 50 кд = 0,08 ср.
Задача 7. Полный световой поток, излучаемый лампой накаливания, равен 6280 лм. Определите силу света этой лампы. I = Ф/ 4 p = 6280 / 4× 3,14 = 500 кд. Задача 8. На книгу перпендикулярно ее поверхности, падают солнечные лучи. Световой поток составляет 37 лм. Определите, какой световой поток будет падать на книгу, если ее отклонить на угол 30°.
Cos 30 = 0,866; Е= Ф/ 4 p;
Задача 9. На хромированную отражающую поверхность падает световой поток 1000 лм. Определите отраженный и поглощенный световые потоки, если коэффициент отражения хрома 0,65. С учетом отсутствия рассеянного излучения, 1000 лм×0,65 = 650 лм (отраженный световой поток). 1000 лм-650 лм = 350 лм (поглощенный поток).
Задача 10. Освещенность поверхности равна 50 лк при падении на нее светового потока 40 лм. Определите площадь освещаемой поверхности.
Задача 11. Определить величину светового потока, если световая энергия за 6 мин равна 3600 лм×с.
Световой поток – величина, равная световой энергии (оцениваемой по зрительному ощущению), проходящей через заданную поверхность за единицу времени: Поэтому для определения светового потока необходимо световую энергию W = 3600 лм*с разделить на время излучения t = 6 мин, т.е. 3600/(6*60) = 3600/360 = 10 (лм).
Задача 12. Определить световую эффективность излучения источника, обладающего световым потоком 15 лм, при расходовании им мощности 5 Вт?
Световая эффективность K = Фn / Фе, где Фn - световая величина светового потока (15 лм); Фе - энергетическая величина светового потока (5 Вт). Ответ: K= 15/ 5 = 3 (лм/Вт)
Задача 13. Определить светимость некоторой поверхности площадью S=0,2 м2, если исходящий от нее световой поток равен Ф=20 лм?
Светимость есть величина, равная отношению светового потока к площади источника света: М = Ф/ S. Поэтому М = 20 / 0,2 = 100 (лм/м2)
|
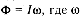– телесный угол. Для определения телесного угла соединим точку O (рис. 2), где находится точечный источник света, если т.A - край стола. Перемещая прямую линию OA вокруг неподвижной точки O, получим прямой конус. Основанием конуса является круг, диаметр которого равен диаметру стола, а высота проходит через центр основания и равна расстоянию от источника света до центра стола. Поместим вершину O полученного конуса в центр сферы радиусом R. Пересекаясь со сферой, боковая поверхность конуса вырезает на ней сегментную поверхность АBD. Площадь сегментной поверхности равна произведению длины окружности большого круга на высоту сегмента, то есть
,
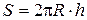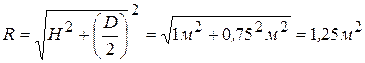
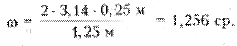
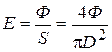, где 
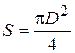площадь поверхности стола. Подставляя числовые значения, получаем:
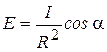
- падения лучей в точку O равен нулю. Следовательно:
.
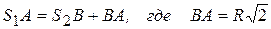
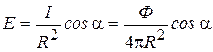Если 
, то cosa=1: Тогда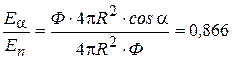
: 
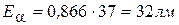
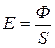
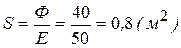
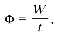где W – количество световой энергии, проходящей через заданную поверхность за время t.
