Нечеткие множества и лингвистические переменные
Термин "нечеткое множество" (fuzzy set) был впервые введен в уже упоминавшейся классической работе Л.А.Заде. Прежде чем дать строгое толкование этого понятия, обратимся к следующему примеру. Допустим, что объектом нашего исследования является множество "взрослых людей", к которому формально можно отнести всех людей, достигших совершеннолетия (18 лет). Если обозначить через переменную
то множество "взрослых людей" А может быть задано с помощью выражения
где X - множество всех возможных значений Другими словами, множество А образуют такие "объекты" ("элементы"), для которых указанная выше функция В то же время, очевидно, что двузначная логика (типа "да" - "нет"), определяемая функцией принадлежности Поэтому более естественным является задание функции принадлежности в виде некоторой непрерывной зависимости (пунктирная кривая на рис.2.1), определяющей плавный переход
Рис.2.1. Графическое представление множества "взрослых людей" из одного крайнего состояния в другое (т.е. от принадлежности элементов рассматриваемому множеству до непринадлежности ему). В данном случае функция принадлежности
называется нечетким (или размытым) множеством. Перечислим основные свойства нечетких множеств. Будем называть носителем А множество тех его элементов
Точка перехода А – это элемент Срез
Высота нечеткого множества А находится как точная верхняя грань (максимум) его функции принадлежности:
Если высота нечеткого множества равна 1, то такое множество называется нормализованным. В том случае, когда высота нечеткого множества А меньше 1 (такое множество называется субнормальным), можно осуществить переход к нормализованному множеству путем деления его функции принадлежности Если носитель нечеткого множества А состоит из единственной точки
где Если носитель А состоит из конечного числа элементов, то для записи такого дискретного множества используется выражение
где числа Заметим, что знак "плюс" в (2.6) обозначает объединение, а не арифметическое суммирование. Обычное (четкое) дискретное множество при такой форме записи можно представить в виде
Возможен и табличный способ задания нечеткого множества А. Например, таблица
обозначает, что носитель А состоит из 5 элементов: Если носитель нечеткого множества А состоит из бесконечного числа точек, например, представляет собой некоторый интервал (а, в) на числовой оси х, то функция принадлежности Рассмотрим пример. Допустим, что для косвенного измерения скорости вращения вала нагруженного электропривода используется выходное напряжение генератора постоянного тока. Известно значение этого напряжения Функция принадлежности
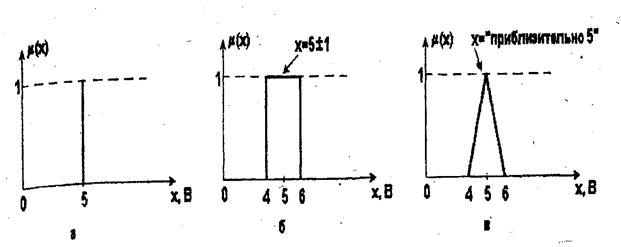
Рис.2.2. Построение функции принадлежности Представленный на рис.2.2, а - в процесс перехода от четкого (т.е. измеренного) значения х = 5 к его "нечеткой" интерпретации х = "приблизительно 5" называется фаззификацией (fuzzyfication). Вопрос о том, как выбирается (или задается) в каждом конкретном случае функция принадлежности Одним из ключевых понятий нечеткой логики является понятие лингвистической переменной. Суть данного понятия состоит в том, что конкретные значения числовой переменной х обычно подвергаются субъективной оценке человеком, причем результат такой оценки выражается на естественном языке. Так, переменная "Рост (высота) человека" может характеризоваться одним из следующих термов (terms), т.е. сжатых словесных описаний: "маленький", "невысокий", "среднего роста", "высокий". Другая переменная – "Скорость движения автомобиля" – может быть "малой", "средней", "большой" и т.д. Каждый из приведенных здесь термов может рассматриваться как символ некоторого нечеткого подмножества в составе полного множества значений х. Переменные, значениями которых являются термы (слова, фразы, предложения), выраженные на естественном языке, называют лингвистическими переменными (linguistic variables). Задать нечеткое подмножество Пример 1. Рассмотрим лингвистическую переменную "Яркость" изображения. Будем полагать, что различные значения физической переменной х яркости (единица измерения кд/м2) могут быть охарактеризованы набором из 5 нечетких подмножеств (значений лингвистической переменной): {"Очень темно", "Темно", "Средне", "Светло", "Очень светло"}. На рис.2.3 показаны функции принадлежности для каждого из этих подмножеств. Допустим, что фактическое значение яркости равно 5,5 кд/м2. Тогда, в соответствии с рис.2.3, это значение относится одновременно к двум термам (подмножествам) - "Средне" и "Светло" - со степенями принадлежности
Рис.2.3. Лингвистическая переменная "Яркость" Пример 2. Рассмотрим процедуру фаззификации (перехода к нечеткости) на примере поставляемой с пакетом fuzzy TECH модели контейнерного крана. Пусть вам, как маститому крановщику, необходимо перегрузить контейнер с баржи на железнодорожную платформу. Вы управляете мощностью двигателя тележки крана, заставляя ее двигаться быстрее или медленнее. От скорости перемещения тележки, в свою очередь, зависит расстояние до цели и амплитуда колебания контейнера на тросе. Вследствие того, что стратегия управления краном сильно зависит от положения тележки, применение стандартных контроллеров для этой задачи весьма затруднительно. Вместе с тем математическая модель движения груза, состоящая из нескольких дифференциальных уравнений, может быть составлена довольно легко, но для ее решения при различных исходных данных потребуется довольно много времени. К тому же исполняемый код программы будет большим и не поворотливым. Нечеткая система справляется с такой задачей очень быстро – несмотря на то, что вместо сложных дифференциальных уравнений движения груза весь процесс движения описывается терминами естественного языка: «больше», «средне», «немного» и т. п. То есть так, будто вы даете указания своему товарищу, сидящему за рычагами управления. В процессе фаззификации точные значения входных переменных преобразуются в значения лингвистических переменных посредством применения положений теории нечетких множеств, а именно – при помощи определенных функций принадлежности. В нечеткой логике значением лингвистической переменной ДИСТАНЦИЯ являются термы ДАЛЕКО, БЛИЗКО и т. д. Для реализации лингвистической переменной необходимо определить точные физические значения ее термов. Пусть, например, переменная ДИСТАНЦИЯ может принимать любое значение из диапазона от 0 до 60 м. Каждому значению расстояния из диапазона в 60 метров может быть поставлено в соответствие некоторое число, от нуля до единицы, которое определяет СТЕПЕНЬ ПРИНАДЛЕЖНОСТИ данного физического значения расстояния (допустим, 10 метров) к тому или иному терму лингвистической переменной ДИСТАНЦИЯ. Расстоянию в 50 метров можно задать степень принадлежности к терму ДАЛЕКО, равную 0,85, а к терму БЛИЗКО - 0,15. Конкретное определение степени принадлежности возможно только при работе с экспертами. При обсуждении вопроса о термах лингвистической переменной интересно прикинуть, сколько всего термов в переменной необходимо для достаточно точного представления физической величины. В настоящее время сложилось мнение, что для большинства приложений достаточно 3 - 7 термов на каждую переменную. Минимальное значение числа термов вполне оправданно. Такое определение содержит два экстремальных значения (минимальное и максимальное) и среднее. Для большинства применений этого вполне достаточно. Что касается максимального количества термов, то оно не ограничено и зависит целиком от приложения и требуемой точности описания системы. Число же 7 обусловлено емкостью кратковременной памяти человека, в которой, по современным представлениям, может храниться до семи единиц информации. Дадим два совета, которые помогут в определении числа термов: - исходите из стоящей перед вами задачи и необходимой точности описания, помните, что для большинства приложений вполне достаточно трех термов в переменной; - составляемые нечеткие правила функционирования системы должны быть понятны, вы не должны испытывать существенных трудностей при их разработке; в противном случае, если не хватает словарного запаса в термах, следует увеличить их число. Как уже говорилось, принадлежность каждого точного значения к одному из термов лингвистической переменной определяется посредством функции принадлежности. Ее вид может быть абсолютно произвольным. Сейчас сформировалось понятие о так называемых стандартных функциях принадлежности (см. рис.).
Стандартные функции принадлежности легко применимы к решению большинства задач. Однако если предстоит решать специфическую задачу, можно выбрать и более подходящую форму функции принадлежности, при этом можно добиться лучших результатов работы системы, чем при использовании функций стандартного вида. Подведем некоторый итог этапа фаззификации и дадим некое подобие алгоритма по формализации задачи в терминах нечеткой логики. Шаг 1. Для каждого терма взятой лингвистической переменной найти числовое значение или диапазон значений, наилучшим образом характеризующих данный терм. Так как это значение или значения являются «прототипом» нашего терма, то для них выбирается единичное значение функции принадлежности. Шаг 2. После определения значений с единичной принадлежностью необходимо определить значение параметра с принадлежностью «0» к данному терму. Это значение может быть выбрано как значение с принадлежностью «1» к другому терму из числа определенных ранее. Шаг 3. После определения экстремальных значений нужно определить промежуточные значения. Для них выбираются П- или Л-функции из числа стандартных функций принадлежности. Шаг 4. Для значений, соответствующих экстремальным значениям параметра, выбираются S - или Z-функции принадлежности.
|

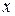 "возраст человека", а функцию
"возраст человека", а функцию  задать следующим образом:
задать следующим образом: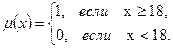

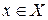 , для которых
, для которых  , не принадлежат множеству А.
, не принадлежат множеству А.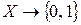 , не учитывает возможного разброса мнений различных субъектов относительно границ исследуемого множества А, влияния чисто биологических факторов, национальных особенностей и т. д.
, не учитывает возможного разброса мнений различных субъектов относительно границ исследуемого множества А, влияния чисто биологических факторов, национальных особенностей и т. д.
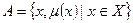
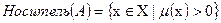
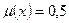 .
. нечеткого множества А – множество элементов
нечеткого множества А – множество элементов 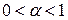 ):
):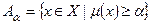

 .
.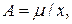
 - степень принадлежности х множеству А.
- степень принадлежности х множеству А.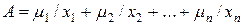 , или
, или 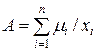
 - степени принадлежности элементов
- степени принадлежности элементов 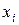 множеству А.
множеству А. или
или 



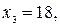
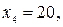
 степени принадлежности которых множеству А равны соответственно: 0,1; 0,3; 0,5; 0,8 и 1,0.
степени принадлежности которых множеству А равны соответственно: 0,1; 0,3; 0,5; 0,8 и 1,0.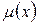 обычно задается графически или в виде аналитической зависимости.
обычно задается графически или в виде аналитической зависимости. . Кроме того, известно, что ошибка такого измерения составляет ±1 В. Тогда переход от четкого значения
. Кроме того, известно, что ошибка такого измерения составляет ±1 В. Тогда переход от четкого значения  к нечеткому множеству " х равно приблизительно 5" осуществляется следующим образом (рис.2.2).
к нечеткому множеству " х равно приблизительно 5" осуществляется следующим образом (рис.2.2).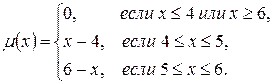
 , соответствующее определенному i -му терму (значению) лингвистической переменной, – это значит задать область определения числовой переменной х и функцию принадлежности элемента х подмножеству
, соответствующее определенному i -му терму (значению) лингвистической переменной, – это значит задать область определения числовой переменной х и функцию принадлежности элемента х подмножеству 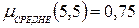 и
и  соответственно.
соответственно.




