Постановка задачи и этапы минимизации логических функций.
ТЕМА 2 Анализ и синтез комбинационных автоматов ЛЕКЦИЯ 3 Минимизация логических функций Вопросы лекции: Постановка задачи и этапы минимизации логических функций. 2. Минимизация комбинационных автоматов.
Литература:
Контрольные вопросы:
1. Постановка задачи и этапы минимизации логических функций
Структурная схема логически (цифровых) устройств может быть получена непосредственно и по ДНФ или СДНФ (КНФ или СКНФ). Однако, этот метод, обеспечивающий правильность функционирования цифровых устройств, требует использования большого числа логических элементов, имеет низкую экономичность и надежность. Во многих случаях удается так удается упростить структурную схему, не изменив логической функции, что видоизмененная схема оказывается горазда проще. Методы такого упрощения называются методами минимизации логических функций. Пример. (Лекция 2, пример 3, функция Упростим эту функцию, используя операции склеивания (распределительный закон)
На практике для представления логических функций чаще всего используется ДНФ (СДНФ). Поэтому в дальнейшем остановимся на этом представлении. Вспомним некоторые определения и введем новые. Дизъюнктивной нормальной формой (ДНФ) логической функции Совершенной дизъюнктивной нормальной формой (СДНФ) логической функции Минимальной д изъюнктивной нормальной формой (МДНФ) функции Задача построения МДНФ носит название минимизации. Она сводится к проблеме выбора базиса (функционально полной системе логических функций) и экономного представления функции в этом базисе. Иногда ставится аналогичная задача построения ДНФ, содержащей минимальной число конъюнкций. Такая ДНФ называется кратчайшей.
|

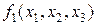 )
)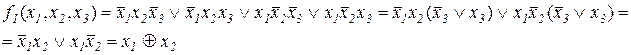 Как видно для реализации исходной логической функции необходимо 8 логических элементов: 3 элемента НЕ, 4 трехвходовых элементов И, четырехвходовый элемент ИЛИ. Для реализации упрощенной формулы необходимо только четыре логических элемента (2 элемента НЕ, 2 двухвходовых элементов И, двухвходовый элемент ИЛИ) или один элемент неравнозначность.
Как видно для реализации исходной логической функции необходимо 8 логических элементов: 3 элемента НЕ, 4 трехвходовых элементов И, четырехвходовый элемент ИЛИ. Для реализации упрощенной формулы необходимо только четыре логических элемента (2 элемента НЕ, 2 двухвходовых элементов И, двухвходовый элемент ИЛИ) или один элемент неравнозначность. называется дизъюнкция различных элементарных конъюнкций.
называется дизъюнкция различных элементарных конъюнкций.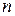 переменных
переменных  называется дизъюнкция элементарных конъюнкций ранга
называется дизъюнкция элементарных конъюнкций ранга 


