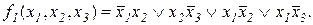Минимизация логических функций методом Квайна-Мак-Класки.
Идея Мак-Класки основана на упрощении процедуры склеивания заменой операций с буквенными выражениями операциями с двоичными числами: каждой конституенте «1» сопоставляется двоичное число, соответствующее номеру набора. Алгоритм поиска по методу Квайна-Мак-Класки рассмотрим на примере. 1. Логической функции 2. Числа, отличающиеся значением только в одном разряде, называются соседними, например, 3. Для облегчения поиска соседних чисел (склеиваемых пар) все числа разбиваются на группы имеющие одинаковое количество единиц (индексы чисел), например,. 4. Склеиваемые пары ищутся в группах, индекс которых различается на единицу, например, 5. Все склеиваемые импликанты помечаются, несклеиваемые являются простыми. 6. При склеивании соседних чисел в разряд с разными значениями ставится прочерк. Для рассматриваемого примера получим 7. В результате получим Ск. ДНФ -
|
соответствуют числа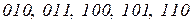 
.
.
; 
.
.
, 
, 
,. 
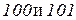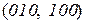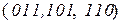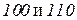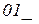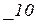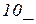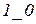. Все полученные наборы имеют одинаковый индекс, следовательно они являются несклеиваемые, их помечаем - они являются простыми импликантами, участвующими в образовании сокращенной ДНФ.
