Понятия об импликантах логических функций

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Логическая функция 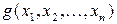называется импликантой логические функции , если все единичные наборы переменных функции 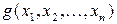являются подмножеством единичных наборов функции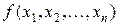

Пример.

В логической функции импликантами являются все конституенты «1» (логическая функция, единичное значение которой определено только на одном наборе переменных): .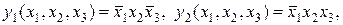

Простой импликантой логической функции 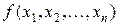называется элементарное произведение всех или части переменных 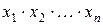, являющееся импликантой логической функции 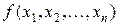, такое, что удалении любого числа сомножителей приведет к получению произведения, не являющегося импликантой.

Пример.

В логической функции 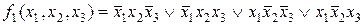, определенной на наборах 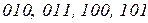, выполним операции склеивания первого и второго, а также третьего и четвертого слагаемых:

простыми импликантами являются произведения , которые определены на наборах и 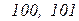, соответственно. Причем, переменная 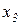для обеих произведений является фиктивной. Удаление любой из переменных в этих конъюнкциях приведет к увеличению числа единичных наборов, следовательно, эти произведения являются простыми импликантами.

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Дата добавления: 2015-09-07; просмотров: 421. Нарушение авторских прав; Мы поможем в написании вашей работы!

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...

Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...

Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...

Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...

Метод Фольгарда (роданометрия или тиоцианатометрия) Метод Фольгарда основан на применении в качестве осадителя титрованного раствора, содержащего роданид-ионы SCN...

Потенциометрия. Потенциометрическое определение рН растворов Потенциометрия - это электрохимический метод исследования и анализа веществ, основанный на зависимости равновесного электродного потенциала Е от активности (концентрации) определяемого вещества в исследуемом растворе...

Гальванического элемента При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов...

Studopedia.info - Студопедия - 2014-2025 год . (0.011 сек.) русская версия | украинская версия