Контрольное задание для студентов 1-го12
Курса
1. Для данных матриц А и В и заданных чисел α, β требуется найти: 1) АВ; 2) αА · В; 3) βА – Е, где Е – единичная матрица; 4) транспонированные матрицы АТ и ВТ.
2. По данной матрице вычислить её определитель следующими способами: 1) разложением по элементам какой-нибудь строки; 2) разложением по элементам какого-либо столбца; 3) методом Гаусса.
3. По заданной матрице А найти её обратную А-1 и проверить равенства А · А-1 = А-1 · А = Е.
4. При заданных матрицах А и В найти неизвестную матрицу Х, удовлетворяющую матричному уравнению АХ = В. 5. Найти общее решение данной однородной системы линейных алгебраических уравнений с помощью её фундаментальной системы решений. 6. При заданных А и В найти общее решение неоднородной системы АХ = В, используя фундаментальную систему решений соответствующей приведённой однородной системы уравнений. 7. Найти общее решение данной системы линейных алгебраических уравнений методом Гаусса. 8. Вычислить ранг заданной матрицы. 9. Заданную систему линейных уравнений исследовать на совместность по критерию совместности (по теореме Кронекера – Капелли) и на определённость. 10. Решить систему линейных алгебраических уравнений следующими способами: 1) по формулам Крамера; 2) матричным методом; 3) методом Гаусса. 11. Данную систему линейных уравнений привести к системе с базисом методом Жордана – Гаусса и найти одно базисное решение. 12. Найти три опорных решения данной канонической системы линейных уравнений методом преобразования однократного замещения. 13. Найти собственные векторы и собственные значения линейного преобразования переменных, заданного матрицей А. 14. Привести данную квадратичную форму к каноническому виду методом ортогональных преобразований. Выяснить, является ли она положительно определённой. 15. Выяснить с помощью критерия Сильвестра, является ли квадратичная форма положительно определённой.
Вариант 1
1. 2. 4.
6. 7.
8. 10. 12.
14.
Вариант 2
1.
2. 4. 6. 8. 10. 12. 14. Вариант 3
1.
2. 4. 6. 8. 10. 12.
14. Вариант 4
1. 2. 4. 6. 8. 10. 12. 14. Вариант 5
1.
2. 4. 6. 8. 10. 12. 14. Вариант 6 1.
2. 4. 6. 8. 10. 12. 14. Вариант 7 1.
2. 4. 6. 8. 10. 12. 14. Вариант 8 1.
2. 4. 6. 8. 10. 12. 14. Вариант 9 1.
2. 4. 6. 8. 10. 12. 14. Вариант 10 1.
2. 4. 6. 8. 10. 12. 14. Вариант 11 1.
2. 4. 6. 8. 10. 12. 14. Вариант 12 1.
2. 4. 6. 8. 10. 12. 14. Вариант 13 1.
2. 4. 6. 8. 10. 12. 14. Вариант 14 1.
2. 4. 6. 8. 10. 12. 14.
Вариант 15 1.
2. 4. 6. 8. 10. 12. 14. Вариант 16 1.
2. 4. 6. 8. 10. 12. 14. Вариант 17 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 18 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 19 1.
2. 4. 6. 8. 10. 12. 14. 15. Вариант 20 1.
2. 4. 6. 8. 10. 12. 14. Вариант 21 1.
2. 4. 6. 8. 10. 12. 14. Вариант 22 1.
2. 4. 6. 8. 10. 12. 14. Вариант 23 1.
2. 4. 6. 8. 10. 12. 14. Вариант 24 1. 2. 4. 6. 8. 10. 12. 14. 15. Вариант 25 1.
2. 4. 6. 8. 10. 12. 14. Вариант 26 1.
2. 4. 6. 8. 10. 12. 14. Вариант 27 1. 2. 4. 6. 8. 10. 12. 14. Вариант 28 1. 2. 4. 6. 8. 10. 12. 14. Вариант 29 1.
2. 4. 6. 8. 10. 12. 14. Вариант 30 1.
2. 4. 6. 8. 10. 12. 14. 12
|

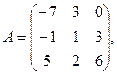
 α = 6, β = 3.
α = 6, β = 3. 3.
3. 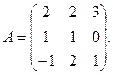
 5.
5. 

 9.
9. 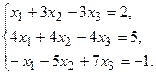
 11.
11. 
 13.
13. 
 15.
15. 
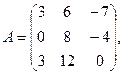
 α = 2, β = 4.
α = 2, β = 4.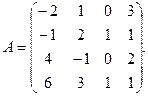 3.
3. 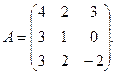
 5.
5. 

 7.
7. 
 9.
9. 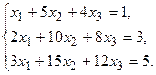
 11.
11. 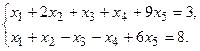
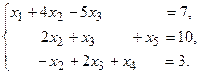 13.
13. 
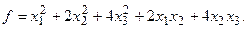 15.
15. 

 α = – 2, β = 5.
α = – 2, β = 5. 3.
3. 
 5.
5. 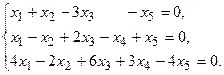
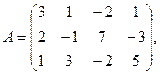
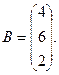 7.
7. 
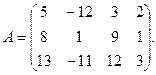 9.
9. 
 11.
11. 
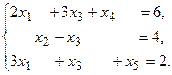 13.
13. 
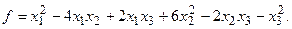 15.
15. 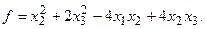

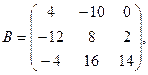 α = 4, β =
α = 4, β = 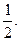
 3.
3. 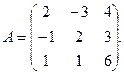
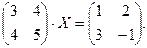 5.
5. 
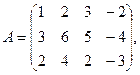
 7.
7. 
 9.
9. 
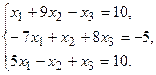 11.
11. 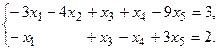
 13.
13. 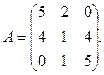
 15.
15. 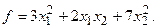

 α = 3, β = 5.
α = 3, β = 5. 3.
3. 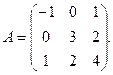
 5.
5. 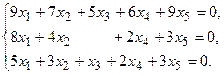
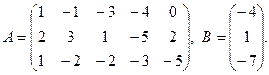 7.
7. 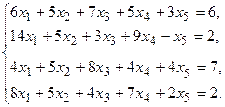
 9.
9. 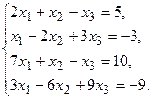
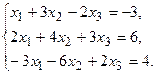 11.
11. 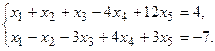
 13.
13. 
 15.
15. 

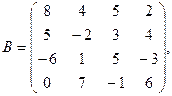 α = – 2, β = 3.
α = – 2, β = 3. 3.
3. 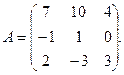
 5.
5. 
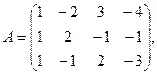
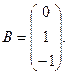 7.
7. 
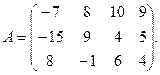 9.
9. 
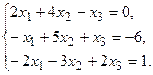 11.
11. 
 13.
13. 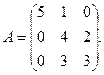
 15.
15. 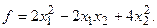

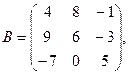 α = – 5, β = 3.
α = – 5, β = 3.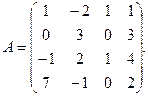 3.
3. 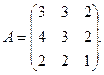
 5.
5. 

 7.
7. 
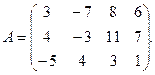 9.
9. 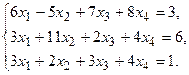
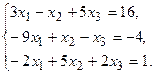 11.
11. 
 13.
13. 
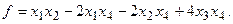 15.
15. 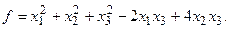

 α = 10, β = – 3.
α = 10, β = – 3. 3.
3. 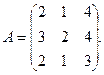
 5.
5. 
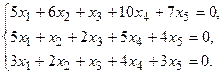

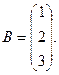 7.
7. 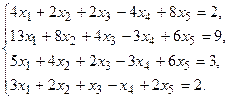
 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 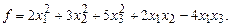

 α = – 3, β = 10.
α = – 3, β = 10. 3.
3. 
 5.
5. 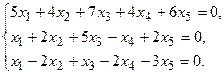
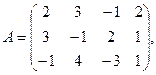
 7.
7. 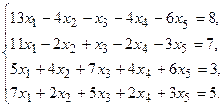
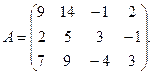 9.
9. 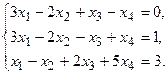
 11.
11. 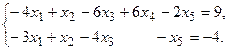
 13.
13. 
 15.
15. 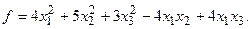
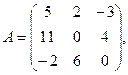
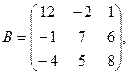 α = – 6, β = 4.
α = – 6, β = 4. 3.
3. 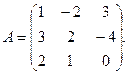
 5.
5. 

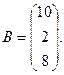 7.
7. 
 9.
9. 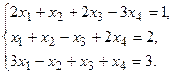
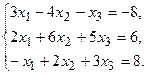 11.
11. 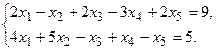
 13.
13. 
 15.
15. 

 α = – 2, β = 3.
α = – 2, β = 3. 3.
3. 
 5.
5. 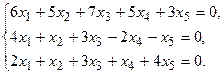

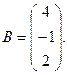 7.
7. 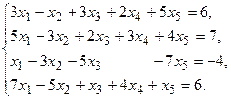
 9.
9. 
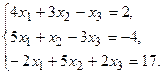 11.
11. 
 13.
13. 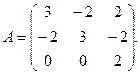
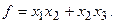 15.
15. 
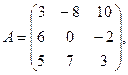
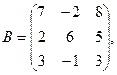 α = 9, β = – 3.
α = 9, β = – 3.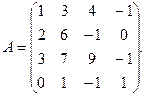 3.
3. 
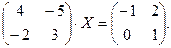 5.
5. 
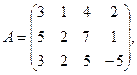
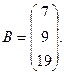 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 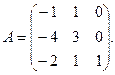
 15.
15. 

 α = – 10, β = – 2.
α = – 10, β = – 2. 3.
3. 
 5.
5. 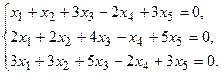
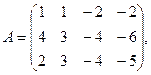
 7.
7. 
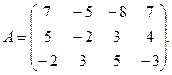 9.
9. 
 11.
11. 
 13.
13. 
 15.
15. 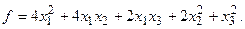
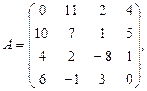
 α = – 2, β = 4.
α = – 2, β = 4. 3.
3. 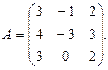
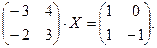 5.
5. 

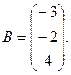 7.
7. 
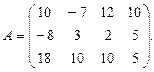 9.
9. 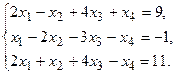
 11.
11. 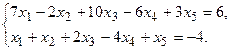
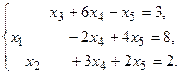 13.
13. 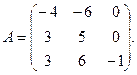
 15.
15. 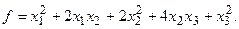

 α = – 9, β = 5.
α = – 9, β = 5. 3.
3. 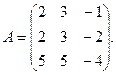
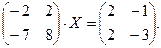 5.
5. 

 7.
7. 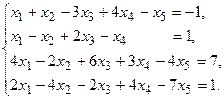
 9.
9. 
 11.
11. 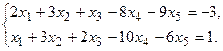
 13.
13. 
 15.
15. 
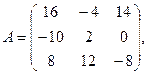
 α =
α =  , β = 10.
, β = 10. 3.
3. 
 5.
5. 
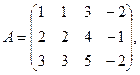
 7.
7. 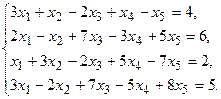
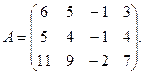 9.
9. 
 11.
11. 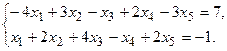
 13.
13. 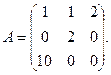
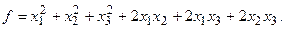 15.
15. 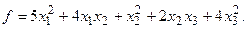

 α = – 4, β = 5.
α = – 4, β = 5. 3.
3. 
 5.
5. 

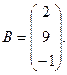 7.
7. 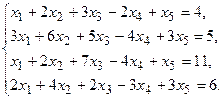
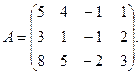 9.
9. 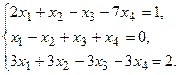
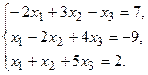 11.
11. 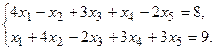
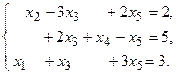 13.
13. 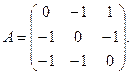

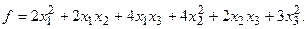
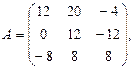
 α =
α =  , β = 4.
, β = 4. 3.
3. 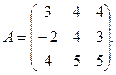
 5.
5. 

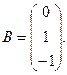 7.
7. 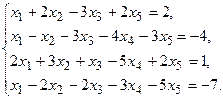
 9.
9. 
 11.
11. 
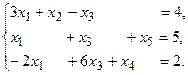 13.
13. 
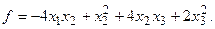


 α = 11, β = 7.
α = 11, β = 7. 3.
3. 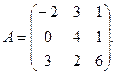
 5.
5. 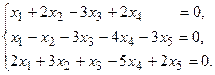

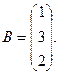 7.
7. 
 9.
9. 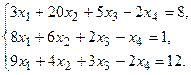
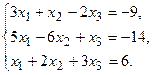 11.
11. 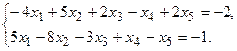
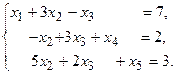 13.
13. 
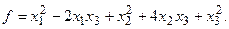

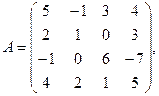
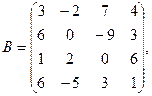 α = 3, β = – 5.
α = 3, β = – 5.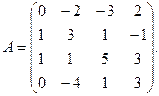 3.
3. 
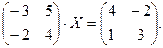 5.
5. 
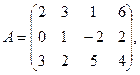
 7.
7. 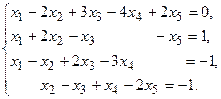
 9.
9. 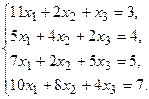
 11.
11. 
 13.
13. 


 α = 3, β = – 2.
α = 3, β = – 2.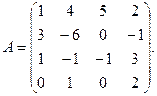 3.
3. 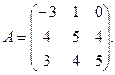
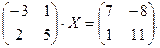 5.
5. 

 7.
7. 
 9.
9. 
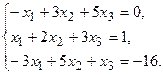 11.
11. 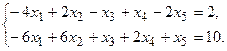
 13.
13. 
 15.
15. 
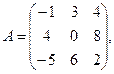
 α = 5, β = –3.
α = 5, β = –3.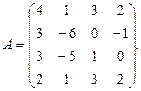 3.
3. 
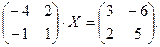 5.
5. 
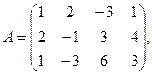
 7.
7. 
 9.
9. 
 11.
11. 
 13.
13. 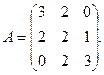
 15.
15. 

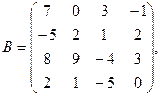 α = 4, β = – 5.
α = 4, β = – 5. 3.
3. 
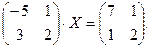 5.
5. 
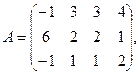

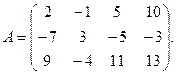 9.
9. 
 11.
11. 
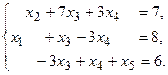 13.
13. 
 15.
15. 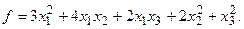
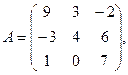
 α = – 7, β = 2.
α = – 7, β = 2.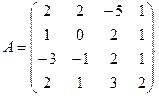 3.
3. 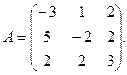
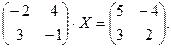 5.
5. 
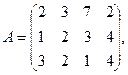
 7.
7. 
 9.
9. 
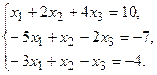 11.
11. 
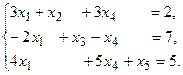 13.
13. 
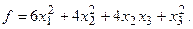
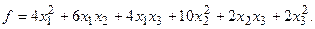
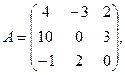
 α = 6, β = – 4.
α = 6, β = – 4. 3.
3. 
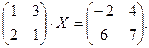 5.
5. 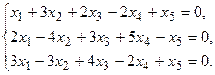
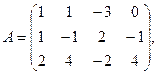
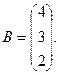 7.
7. 
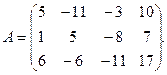 9.
9. 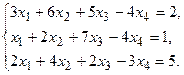
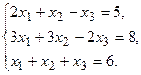 11.
11. 
 13.
13. 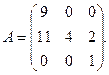
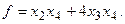 15.
15. 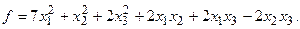

 α = 8, β = – 3.
α = 8, β = – 3. 3.
3. 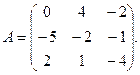
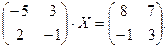 5.
5. 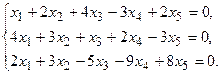

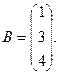 7.
7. 
 9.
9. 
 11.
11. 
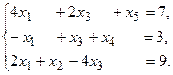 13.
13. 
 15.
15. 

 α = – 5, β = 2.
α = – 5, β = 2. 3.
3. 
 5.
5. 

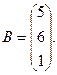 7.
7. 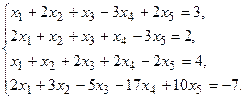
 9.
9. 
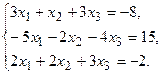 11.
11. 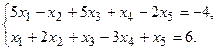
 13.
13. 
 15.
15. 
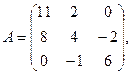
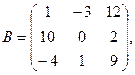 α = 6, β = –2.
α = 6, β = –2.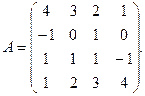 3.
3. 
 5.
5. 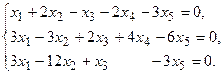
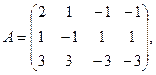
 7.
7. 
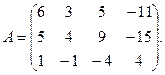 9.
9. 
 11.
11. 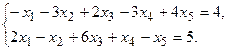
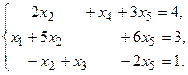 13.
13. 
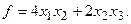 15.
15. 
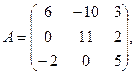
 α = 3, β = 4.
α = 3, β = 4.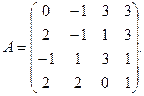 3.
3. 
 5.
5. 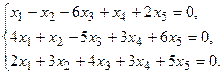
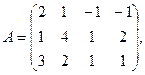
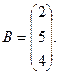 7.
7. 
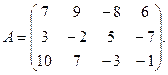 9.
9. 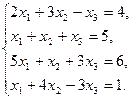
 11.
11. 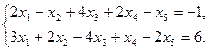
 13.
13. 
 15.
15. 
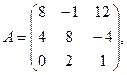
 α = 5, β =1/2.
α = 5, β =1/2. 3.
3. 
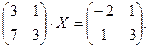 5.
5. 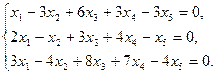

 7.
7. 
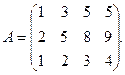 9.
9. 
 11.
11. 
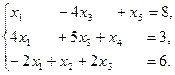 13.
13. 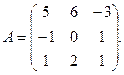
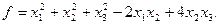 15.
15. 



