Применить тест ранговой корреляции Спирмена для оценки гетероскедастичности
Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы о наличии гетероскедастичности осуществляется отдельно для каждой из них. Значения хi и модуль εiранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
где di — разность между рангами хi и εi, i = 1, 2,..., п; п — число наблюдений. Выдвигается нулевая гипотеза о равенстве коэффициента корреляции Для проверки гипотезы рассчитывается статистика Стьюдента:
Если расчетное значение t превышает табличное с числом степеней свободы v=n-2, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции
Для присвоения ранга значениям факторов и остатка воспользуемся функцией РАНГ (число; ссылка; порядок). Число – это число, для которого определяется ранг; Ссылка – это массив или ссылка на список чисел. Нечисловые значения в списке игнорируются; Порядок – это число, определяющее способ упорядочения. § Если порядок равен 0 или опущен, то Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке убывания. § Если порядок – любое не нулевое число, то Excel определяет ранг числа так, как если бы ссылка была списком, отсортированным в порядке возрастания.
Ранжируем значения фактора х3 и значения остатков. Ввод аргументов статистической функции РАНГ представлен на рисунке 6.
Рисунок 6 – Диалоговое окно функции РАНГ
Рисунок 7 – Результаты расчета коэффициента ранговой корреляции Спирмена для х3 и ε;
Коэффициент ранговой корреляции Спирмена для х3 и ε; составляет Проверим значимость полученного коэффициента с помощью t-статистики Стьюдента: По таблице распределения Стьюдента определили tкр(0,05; v=18) = 2,101. Так как tрасч < tкр, то гипотеза о равенстве нулю коэффициента корреляции Проверка гипотезы о наличии гетероскедастичности для фактора х4.
Рисунок 8 – Результаты расчета коэффициента ранговой корреляции Спирмена для х4 и ε;
Коэффициент ранговой корреляции Спирмена для х4 и ε; составляет t-статистика Стьюдента: Так как tрасч < tкр, то гипотеза о равенстве нулю коэффициента корреляции
3. Применить тест Голдфельда-Квандта.
Тест Голдфелда-Квандта состоит в следующем: 1. Все п наблюдений упорядочиваются по величине той независимой переменной, относительно которой есть подозрение на гетероскедастичность. 2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (п -2k), k соответственно. 3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Рассчитывается сума квадратов остатков по первой и третьей подвыборки: 4 Для сравнения соответствующих дисперсий строится следующая F-статистика:
При сделанных предположениях относительно случайных отклонений, построенная F-статистика имеет распределение Фишера с числами степеней свободы v1=v2=k-m-l. Если то гипотеза об отсутствии гетероскедастичности отклоняется.
Применим тест Голдфелда-Квандта отдельно для каждой переменной. Для фактора х3. Для ранжирования значений фактора х3 и установления соответствующего y и х4 можно воспользоваться Данные / Сортировка списков Рекомендуется данные для сортировки поместить в новый лист т.к. ячейки переупорядочиваются в соответствии с заданным порядком сортировки.
Рисунок 9 – Результат сортировки значений факторов по фактору х3
Разобьем 20 наблюдений на 3 подвыборки объемами 8: 4: 8 соответственно. Для первой и третьей рассчитаем уравнения регрессии и сумму остатков. Результаты расчетов представлены на рисунке 10 - 11.
Рисунок 10 – Результат применения инструмента Регрессия для первой подвыборки
Рисунок 11 – Результаты вычислений суммы квадратов отклонений для первой и третьей подвыборок, упорядоченных по х3
Так как
Аналогично проверим гипотезу об отсутствии гетероскедастичеости для х4.
Рисунок 11 – Результаты вычислений суммы квадратов отклонений для первой и третьей подвыборок, упорядоченных по х4
Так как
|


 для генеральной совокупности нулю, т.е. Н0:
для генеральной совокупности нулю, т.е. Н0: 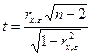


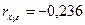 .
. .
.
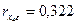 .
. .
. ,
,  .
.

 (по возрастанию). В диалоговом окне «Сортировка диапазона» в строке «Сортировать по» выберите фактор, по которому следует упорядочить данные, в нашем случае х3.
(по возрастанию). В диалоговом окне «Сортировка диапазона» в строке «Сортировать по» выберите фактор, по которому следует упорядочить данные, в нашем случае х3.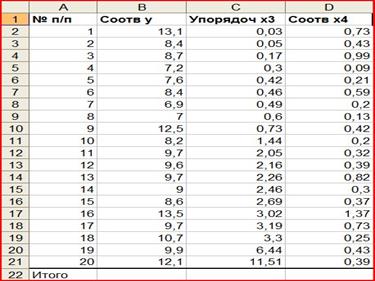


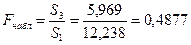

 то гипотеза об отсутствии гетероскедастичности для х3 принимается.
то гипотеза об отсутствии гетероскедастичности для х3 принимается.

 то гипотеза об отсутствии гетероскедастичности для х3 не отклоняется.
то гипотеза об отсутствии гетероскедастичности для х3 не отклоняется.


