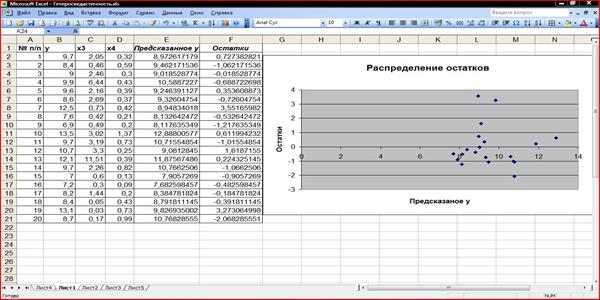
Построить график остатков в зависимости от значений переменных и их комбинации
Для построения графика по оси абсцисс откладываются значения xi объясняющей переменной X (либо линейной комбинации объясняющих переменных
а по оси ординат либо отклонения εi либо их квадраты
Найдем остатки для уравнения регрессии. Для нахождения остатков а) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК; б) заполните диалоговое окно ввода данных и параметров ввода как показано на рисунке 3: Входной интервал Y – диапазон, содержащий данные результативного признака; Входной интервал Х – диапазон, содержащий данные факторов, входящих в модель; Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет; Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист - можно задать произвольное имя нового листа; Остаток - флажок, указывает вывод остатков
Рисунок 1 – Диалоговое окно функции Регрессия для определения остатков
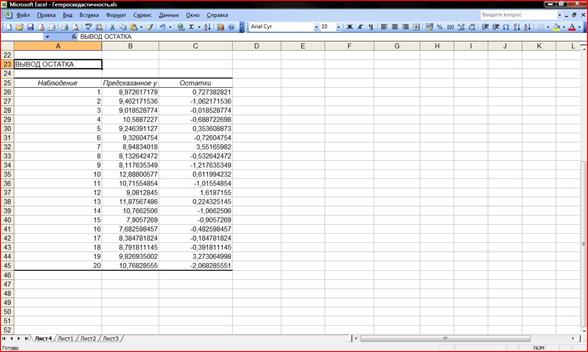
Рисунок 2. Вывод остатка для уравнения регрессии
Построим графики остатков для линейной комбинации факторов, т.е.
Рисунок 3 – Распределение остатков для линейной комбинации факторов
Рисунок 4 – Распределение остатков для фактора х3
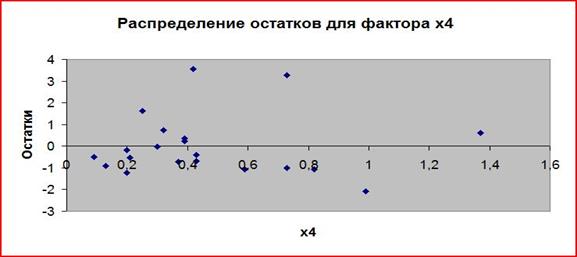
Рисунок 5 – Распределение остатков для фактора х4 Графики показывают, что колеблемость остатков неодинакова при разных значениях
|


 , i = 1, 2,..., п. Если все отклонения
, i = 1, 2,..., п. Если все отклонения 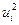 от значений переменной X и их постоянстве, т.е. в этом случае выполняются условия гомоскедастичности.
от значений переменной X и их постоянстве, т.е. в этом случае выполняются условия гомоскедастичности. можно воспользоваться инструментом анализа данных Регрессия. Порядок действий следующий:
можно воспользоваться инструментом анализа данных Регрессия. Порядок действий следующий:
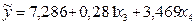
 и отдельно по каждому фактору
и отдельно по каждому фактору  и
и  .
.